软件设计师第1部分计算机科学基础一
09年5月软考数据库系统工程师专家参考答案(上午)
09年5月软考数据库系统工程师专家参考答案(下午)
当部件(1)~(3)正常时,系统正常,则此概率为:0.85*0.9*0.95=0.7268。
如图b时,则部件2的可靠性为:1-(1-0.8)*(1-0.85)=0.97。同样,可得部件C正常的概率为0.99则系统可靠性为:0.85×0.97×0.99=0.816。
●在对二叉树进行前序、中序和后序遍历时,最适合采用的方法是(28)。
查找树中,由根结点到所有其他结点的路径长度的总和称为(29),而(30)使上述路径长度总和达到最小,它一定是(31)。
在关于树的几个叙述中,只有(32)是正确的。
(28)A.队列操作
B.迭代程序
C.递归程序
D.栈操作
(29)A.路径和
B.深度和
C.总深度
D.内部路径长度
(30)A.丰满树
B.B+-树
C.B-树
D.穿线树
(31)A.B-树
B.平衡树
C.非平衡树
D.穿线树
(32)A.平衡树一定是丰满树
B.m阶B一树中,每个非叶子结点的后代个数≥[m/2]
C.m阶B-树中,具有k个后代的结点,必含有k-1个键值
D.用指针方式存储有n个结点二叉树,至少要有n+1个指针
答案:(28)C(29)D(30)A(31)B(32)C
解析:前序、中序和后序遍历法最适合采用递归算法来实现。查找树中,由根结点到所有其他结点的路径长度的总和称为内部路径长度,而使内部路径长度总和达到最小的树称为车满树。它必一定是平衡树,因为如果丰满树如果不是平衡树。则调整其成为平衡树后.。被调整结点高度必定减小,则内部路径长度随之减小。那么原树就不是丰满树。产生矛盾,得证。m阶B-树中,若结点含有k-1个键值,则具有k个后代。
●查找二叉树中,结点值大于左子树所有结点值,而小于右结点所有结点值。现在有一棵查找二叉树,它的结点A、B、c、D、E、F依次存放在一个起始地址为a(假定地址以字节为单位顺序编号)的连续区域中,每个结点占6个字节:前四个字节存放结点值,后二个字节依次放左指针、右指针。若该查找二叉树的根结点为D,则它的一种可能的前序遍历为(33),相应的层次遍历为(34)。在以上两种遍历情况下,结点C的左指针的存放地址为(35),它的内容为(36)。结点C的右指针的内容为(37)。
(33)A.DAFCBE
B.DFEACB
C.ADBCFE
D.DACBEF
(34)A.DAECFB
B.DFACEB
C.ABCFDE
D.DEFACB
(35)A.a+15
B.a+16
C.a+18
D.a+19
(36)A.a+6
B.a+10
C.a+14
D.a+18
(37)A.a+4
B.null
C.a+12
D.a+16
答案:(33)D(34)A(35)B(36)A(37)B
解析:可能的前序遍历为DACBEF。如图示。则其层次遍历为DAECFB。
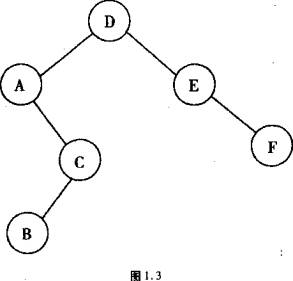
C结点左指针指向B的首地址,即为a+6。C结点左指针的地址为C的第五字节,即a+12+4=a+16。结点A的右子树为空,右指针为null。
●一般来说,递归算法的执行过程可先后分成两个阶段,它们是(38)和(39)。
(38)A.枚举
B.试探
C.递推
D.分析
(39)A.返回
B.合成
C.回溯
D.回归
答案:(38)C(39)D
解析:递归算法的执行过程可分递推和回归两个阶段。在递推阶段,把较复杂的问题(规模为n)的求解推到比原问题简单一些的问题(规模小于n)的求解。回归阶段,当获得最简单情况的解后,逐级返回。依次得到稍复杂问题的解。
●当求解一个问题既可以用递归算法,也可以用递推算法时,我们优先考虑(40)算法,因为(41)。
(40)A.递归
B.递推
C.先递归后递推
D.先递推后递归
(41)A.递归的效率比递推高
B.递归易于问题求解
C.递推的效率比递归高
D.递推宜于问题分解
答案:(40)B(41)A
解析:递归算法不断进行函数调用和返回,需要使用堆栈保存返回地址,回归时需要弹栈回到调用函数中。所以耗费资源(时间,空间)较多,在递推、递归都可以使用的时候,使用递推可以获得更高的效率。
●数据结构中的贪心算法的特点是(42)。
(42)A.求取全部可行解
B.只求最优
C.不求最优,只求满意
D.求取全部最优解
答案:(42)C
解析:贪心算法是一种不追求最优解。只希望得到当前满意解的方法。
●二一十进制编码是一种使用4位二进制数表示一位十进制数的方法,在用二进制加法器求和需要特殊处理,当和的本位十进制数二一十进制编码小于等于1001且向高位无进位时(43);当和小于等于1001且向高位有进位时,(44);当和大于1001时,(45)。
(43)~(45)A.不需修正
B.加6修正
C.减6修正
D.无法判别
答案:(43)A(44)B(45)B
解析:二一十进制编码采用0001表示十进制1,0010表示十进制2,依次类推,1001表示十进制9。十进制运算时,当相加两数之和小于等于9(1001)时,可以直接相加,不需要修正;当大于9时便产生进位,直接相加得到时无效的编码,这时需对和数进行加6修正。因为4位二进制数能表示16个码元,而十进制数只有0到9十个码元。修正时加6,恰好能得到正确的十进制码元。例如1+9=10,正确码元为0000。二进制0001和1001直接相加得到1010。加上6即O110后。得到0000。
●“进位”位移入被操作数的最高位,其余所有位接收其相邻高位值,最低位舍去的操作是(46)指令。被操作数的最高位保持不变,其余所有位接收其相邻高位值,最低位移到“进位”位中的操作是(47)指令。在程序执行过程中改变按程序计数器顺序读出指令的指令属于(48)。实际地址是程序计数器的内容加上指令中形式地址值的寻址方式是(49)。特权指令在多用户、多任务的计算机系统中必不可少,它主要用于(50)。
(46)、(47)A.逻辑右移
B.算术右移
C.乘2运算
D.除2运算
(48)A.传送指令
B.转移指令
C.输入输出指令
D.特权指令
(49)A.相对寻址
B.直接寻址
C.基址寻址
D.变址寻址
(50)A.系统硬件自检和配置
B.检查用户的权限
C.用户写汇编程序时调用
D.系统资源的分配和管理
答案:(46)A(47)D(48)B(49)A(50)D
解析:逻辑右移指所有位右移,最低位舍去。若最高位不变,则为算术运算,具体操作视相应情况而定。转移指令改变程序计数器中顺序读出指令的地址值。使程序发生跳转。相对寻址地址值是当前程序计数器的值与指令中偏移量的和。特权指令用于对系统资源的管理和分配。
●算法中的每一条指令必须有确切的含义,并且在任何条件下,算法只有唯一的一条执行路径,这句话说明算法具有(51)特性。
(51)A.正确性
B.确定性
C.可行性
D.健壮性
答案:(51)B
解析:算法具有有穷性、确定性、可行性、输入、输出五个特点。其中算法中的每一条指令必须有确切的含义,并且在任何条件下。算法只有唯一的一条执行路径说明的是算法的确定性。
●排序算法中的快速排序算法采用的思路是(52)。
(52)A.回溯法
B.分治法
C.动态规划
D.分支定界法
答案:(52)B
解析:快速排序的基本思想是:按照某个基准元素,通过一轮排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比基准元素小:另外一部分的所有数据都比基准元素大,然后再按此方法对这两部分数据分别进行快速排序。整个排序过程可以递归进行,以此达到整个数据变成有序序列。
●哈夫曼(Huffman)编码是一种常用的压缩编码方法,它可以用来构造具有(53)的二叉树,这是一种采用了(54)策略的算法。
(53)A.后缀码
B.最优后缀码
C.前缀码
D.最优前缀码
(54)A.贪心
B.回溯
C.递推
D.分治
答案:(53)D(54)A
解析:哈夫曼(Huffman)编码是一种常用的压缩编码方法,是Huffman于1952年为压缩文本文件建立的。它的基本原理是频繁使用的数据用较短的代码表示,较少使用的数据用较长的代码代替,每个数据的编码各不相同。这些代码都是二进制码,且编码的长度是可变的。编码必须保证不能出现一个码字和另一个的前几位相同的情况。Huffman编码算法具体实现是:首先统计出每个符号出现的频率,然后把上述频率按从小到大的顺序排列。每一次选出最小的两个值,作为二叉树的两个叶子节点,将和作为它们的根节点,这两个叶子节点不再参与比较,新的根节点参与比较。重复上一步,直到最后得到和为1的根节点。将形成的二叉树的左节点标0,右节点标1。把从最上面的根节点到最下面的叶子节点途中遇到的0,1序列串起来,就得到了各个符号的编码。
●二分查找是查找算法中效率非常高的算法,当用递归算法实现n个不同元素构成的有序序列的二分查找,使用的递归工作栈的最小容量应为(55)。
(55)A.Inn
B.[n/2]
C.[log2n]
D.[log2(n+1)]
答案:(55)D
解析:将该有序序列做成一棵完全的二叉查找树,树的高度即为查找失败时进行递归调用次数最多的情况,
即log2(n+1)的整数部分值。
●函数的渐进时间是考虑当问题规模趋于无穷时,函数岁时间变化的趋势,下述函数中渐进时间最小的是(56)。
(56)A.T1(n)=3nlog2n-100log2n
B.T2(n)=2nlog2n-100log2n
C.T3(n)=n2—100log2n
D.T4(n)=nlog2n+100log2n
答案:(56)D
解析:对函数的渐进时间影响最大的是最高数量级,若相同则必须进一步考虑渐进表达式中的常数因子,通过比较不难得出T4(n)=nlog2n+100log2n渐进时间最小。
●写出每种算法第一趟排序后得到的结果:快速排序(选第一个记录为基准元素)得到(57),希尔排序(增量为5)得到(58),堆排序得到(59),二路归并排序得到(60),链式基数(基数为10)排序得到(61):关键字(12,2,16,30,8,28,4,10,20,6,18),递增排序。
(57)A.10,6,18,8,4,2,12,20,16,30,28
B.6,2,10,4,8,12,28,30,20,16,18
C.2,4,6,8,10,12,16,18,20,28,30
D.6,10,8,28,20,18,2,4,12,30,16
(58)A.2,4,6,8,10,12,16,18,20,28,30
B.6,2,10,4,8,12,28,30,20,16,18
C.12,2,10,20,6,18,4,16,30,8,28
D.30,10,20,12,2,4,16,6,8,28,18
(59)A.30,28,20,12,18,16,4,10,2,6,8
B.20,30,28,12,18,4,16,10,2,8,6
C.2,6,4,10,8,28,16,30,20,12,18
D.2,4,10,6,12,28,16,20,8,30,18
(60)A.2,12,16,8,28,30,4,6,10,18,20
B.2,12,16,30,8,28,4,10,6,20,18
C.12,2,l6,8,28,30,4,6,10,28,18
D.12,2,10,20,6,18,4,16,30,8,28
(61)A.10,6,18,8,4,2,12,20,16,30,28
B.12,2,10,20,6,18,4,16,30,8,28
C.2,4,6,8,10,12,16,18,20,28,30
D.30,10,20,12,2,4,16,6,8,28,18
答案:(57)B(58)C(59)C(60)B(61)D
解析:希尔排序的基本思想:将整个无序序列分割成若干小的子序列分别进行插入排序。序列分割方法:将相隔某个增量h的元素构成一个个子序列。在排序过程中,逐次减小这个增量,最后当h减到1时,进行一次插入排序,排序就完成。
堆排序的基本思想:对一组待排序记录,首先把它们按堆的定义排成一个序列(即建立初始小或大堆),输出顶端最小或者最大元素,然后将剩余的关键字再调整成新堆。便得到次小或者次大的关键字。如此重复进行,直至全部关键字排成有序序列。
二路归并排序的基本思想:将两个有序文件合并成一个新的有序文件。它是把一个有n个记录的无序文件看成是由n个长度为l的有序文件组成的文件,然后进行两两归并。得到(n/2)个长度为2或1的有序文件。再两两归并,如此重复,直至全部有序。
基数排序的基本思想是:首先按最低有效位的值把n个关键宇分配到r个队列中,然后从小到大将各队列中关键字再依次收集起来;接着再按次低有效位的值把刚刚收集起来的关键字分配到r个队列中。重复上述过程,直至最高有效位,这样便得到一个从小到大的有序序列。队列采用链式存储分配时。称为链式基数排序。
●AOE(Activity On Edge)网中的关键路径是指(62)。
(62)A.最长的回路
B.最短的回路
C.从源点到汇点(结束顶点)的最短路径
D.从源点到汇点(结束顶点)的最长路径
答案:(62)D
解析:AOE(Activity On Edge)网是边表示活动的网。它是一个带权的有向无环图,顶点表示事件。弧表示活动,权表示活动持续的时间。通常AOE网用来估算工程完成的时间。完成工程的最短时间是从开始点到完成点的最长路径长度(关键路径),即路径上各活动持续时间之和。
●以下关键字序列中不符合堆定义的是(63)。
(63)A.(202,187,200,179,182,162,184,142,122,112,168)
B.(202,200,187,184,182,179,168,162,142,122,112)
C.(202,187,142,179,182,162,168,200,184,112,122)
D.(112,122,142,162,168,179,182,l84,187,200,202)
答案:(63)D
解析:堆的定义如下:具有n个元素的序列(h1,h2…,hn),当且仅当满足(hi>=h2i。hi>=2i+1)或(hi<=h2i,hi<=2i+1)(i=1,2…,n/2)时称之为堆,前者称为最大堆,后者称为最小堆。根据此定义判断。C不是堆。
●一个具有167个结点的完全二叉树,其叶子结点个数为(64)。
(64)A.83
B.84
C.85
D.86
答案:(64)B
解析:完全二叉树中只有度为0和度为2的结点。设为n0和n2,于是总结点数为no+n2。度为2的结点衍生出2个子结点。度为0的结点没有子结点;根结点不是任何点的子结点,所以结点总数还可以表示为2n2+1。于是得到等式nO+n2=2n2+1,推出nO=n2+1。总结点数=2n0-1。本题中。总结点数为167,得nO=84,即叶子结点个数为84。
●若一个森林(非连通无向图)具有n个结点、k条边(n>k),则该森林中必有(65)棵树。(65)A.k
B.n
C.n-k
D.n+k
答案:(65)C
解析:设该森林共有m棵树,每棵树有ni个结点,根据树的性质可得:
1.n=n1+n2+r13…+nm
2.k=(n1-1)+(n2-1)+(n3-1)……+(nm-1)
上面两式相减得n-k=1+1+1+1……=m。而m是树的个数。
●若G是一个具有28条边的非连通无向图(不含自回路和多重边),则图G至少有(66)个顶点。
(66)A.11
B.10
C.9
D.8
答案:(66)C
解析:G是一个非连通无向图,则G至少有2个连通分量。顶点数目最少时,即顶点容纳的边最多,则连通分量比是完全图。8个顶点形成的完全图可容纳36条边,再加一个自成一个连通分量的顶点,所以该图至少有9个点。