《Algorithms》 学习笔记（更新中）
Charpter 0：Prologue
1、算法的时间复杂度是我们选择算法的主导要素，但决不是唯一要素。其它考虑的因素还包括：算法对存储空间的需求、算法实现的难度等等。

2、算法复杂度的表示法：here are some commonsense rules that help simplify function by omitting dominated terms:



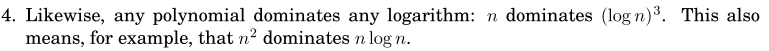
3、Fibonacci数列的求法：递归求解，最直观的想法，指数级复杂度动态规划，从底至顶矩阵求解，能求出通项公式（要线性代数基础，需要求解A^n，A为2*2矩阵，需要的步骤：求特征根、求线性无关特征向量、求P，P逆和对角矩阵、矩阵运算）
4、Whenever we have a algorithm, there are three questions we always ask about it:Is it corrent?How much time does it take, as a function of n?And can we do better?

Chapter 1：Algorithm with numbers
1、二进制乘法的两个算法：
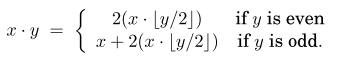这两个算法本质上是一样的。讲到分治的时候，还会介绍新的算法。


2、乘法运算、指数模运算、欧几里得最大公约数：



3、欧几里得算法的几个引理：if a >= b, then a mod b < a/2if d divides both a and b, and d = ax + by for some integers x and y(may be negative) , then necessarily d = gcd(a,b)
4、模除法：gcd(a,N) = 1(即互质) <==> 存在x，使得ax ≡ 1 (mod N) （可用反证法证明）

5、素性测试：最naive的想法：用 2到根号n 除n

费马小定理，通过费马测试的数不一定都是素数；
引理：如果存在一个相对N为素数的a使得 a^(N-1) ≠ 1 mod(N), 则小于N的所有数里面至少有一半（N/2）个 满足这种条件的数。
根据引理：P(return yes when N is not prime) ≤ 1/2
所以只需在选取k个a，就可以使出错概率减小到1/ (2^k) (以上分析都不考虑Carmichael number)
以下是伪码：
附：当a = 2, n≤25*10^9时，费马素性测试的出错情况：（出错概率随着要测试的数的长度的增加而快速下降）


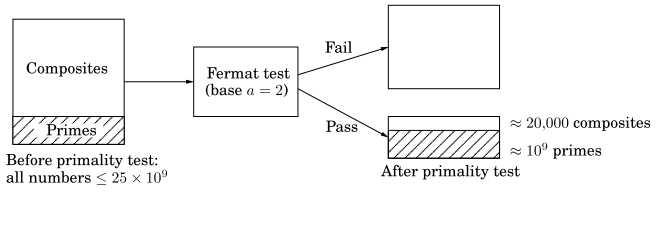
6、密码学原理：对发出的信息进行扰乱，使人读不懂其内容，而接收信息的人按照事先约定的某种方式讲扰乱的信息进行复原，然后即可读懂。分为 私匙协议 和 公匙协议(数论) 。