《Practical WPF Charts and Graphics 》翻译——之八

旋转

假设你想将一个对象顺时针旋转θ角。首先，假设你有了一个点（x1,y1），你想旋转θ角来得到点(x2,y2)，如图2-3所示：

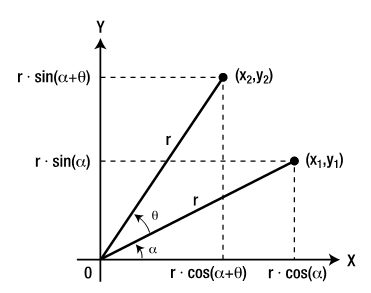
图2-3 从点（x1,y1）旋转到(x2,y2)

从点到原点的距离记为r。于是我们得到下面的关系：

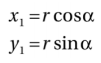
点（x2,y2）是另外一个角度θ旋转得到的同样的点。既然这个点也有一个到原点的距离r，它的坐标可以表示为

将x1=rcosα和y1=rsinα带入前面的方程有

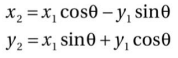
用矩阵的形式表示，将点（x1,y1）旋转到(x2,y2)可得到下面的旋转矩阵：

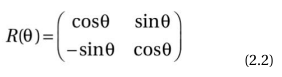
平移

为了平移一个对象，你可以简单的给构成对象的点的X和Y坐标增加一个偏移量：

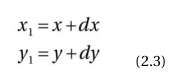
尽管平移看起来简单，但是它却不能用变换矩阵表示。可以将拉伸，反射和旋转表示成矩阵，而把平移却别表示。然而，这样做将会导致很痛苦的簿记（bookkeeping），特别是一个包含很多变换的应用程序里。你可以使用一种将计算移到更高维度的技术来替代。这种技术允许你一致和同样地对待每一个不同的变换。这个叫做齐次坐标系的方法，已经成为几乎每一个图形程序的标准。在下面的章节里，会允许里通过矩阵操作所有变换。

齐次坐标系

我们期望所有2D空间的变换，包括拉伸、反射、旋转和平移，如果在齐次坐标系里表示点，都能相同地对待。齐次坐标系首先在几何学中被引进，随后被应用到图形呈现里。

在齐次坐标系里，你添加第三个坐标到一个点。每一个点被表示成三个坐标（X,Y,W）而不是一对坐标(X,Y)。如果W坐标非零，你可以除以它；（X,Y,W）和(X/W,Y/W,1)是相同的表示。当W非零的时候，你可以正常表示这个除法，数X/W和Y/W通常叫做齐次坐标系里的点坐标。当W=0的时候叫做无穷处的点。

既然2D空间的向量和点现在是3个元素的列向量，乘以一个向量来产生另一个向量的变换矩阵，应该是3*3的了。

齐次坐标系里的变换

在齐次坐标系中，一个变换可以表示成下面的形式：

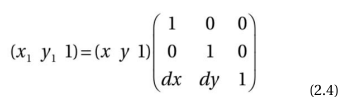
这个变换可以用不同方式表示成

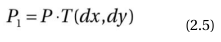
这里P和p1分别表示点(x,y)和(x1,y1)，T(dx,dy)是下面的变换矩阵：

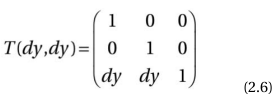
如果一个点P通过T(dx1,dy1)平移到p1，然后被T(dx2,dy2)平移p2会发生什么？结果就像你期望的，是网状的平移T(dx1+dx2,dy1+dy2)。这可以通过下面的定义证明：

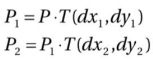
通过前面的方程我们可以得到

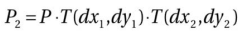
矩阵得到T(dx1,dy1) T(dx2,dy2)是

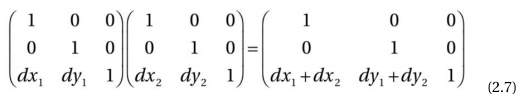
网状平移确实是T(dx1+dx2,dy1+dy2)。