分治法常见题目

递归与分治策略描述的思想是将一个难以直接解决的大问题分割成一些规模较小的相同问题，以便各个击破，分而治之。以下简要介绍几种运用该方法解决的著名问题，以备学习复习笔试面试之用。这些内容包括：

1.汉诺塔问题

2.棋盘覆盖

3.循环赛日程表

4.二分搜索

5.快速排序

6.归并排序

下面逐一描述：

1.汉诺塔问题

?问题描述：有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：

每次只能移动一个圆盘；大盘不能叠在小盘上面。提示：可将圆盘临时置于B杆，也可将从A杆移出的圆盘重新移回A杆，但都必须遵循上述两条规则。

问：如何移？最少要移动多少次？

解法：

#include <iostream>using namespace std;int count=0;//移动杆的显式表示void Move(int i,char a,char c){cout<<"第"<<++count<<"次：将"<<i<<"号盘子从"<<a<<"移动至"<<c<<endl;}//在该函数中，n表示盘子的个数(按起始杆由上到下依次编号1...n)//a表示起始杆，b表示中转杆，c表示目的杆void Hanoi(int n,char a,char b,char c){if (n==1) Move(1,a,c);else{Hanoi(n-1,a,c,b);//将上面的n-1个盘子从a移动到b,c作为辅助Move(n,a,c);//将第n个盘子由a移动到cHanoi(n-1,b,a,c);//将剩下的n-1个盘子从b移动到c上，a作为辅助}}int main(){Hanoi(4,'A','B','C');return 0;}

结果截图：

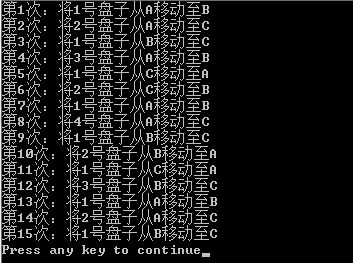
2.棋盘覆盖

问题描述：在一个 2^k * 2^k（k>=1） 个方格组成的棋盘中，若恰有一个方格与其它方格不同，则称该方格为一特殊方格，称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ，有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。

在棋盘覆盖问题中，要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格，且任何 2 个 L 型骨牌不得重叠覆盖。易知，在任何一个 2^k * 2^k 的棋盘中，用到的 L 型骨牌个数恰为 (4^k-1)/3 。

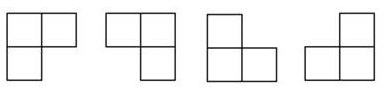
解法：

#include <iostream>#define MAX_SIZE 8using namespace std;int tile = 0;//表示L型骨牌编号int Brand[MAX_SIZE][MAX_SIZE];//表示整个棋盘//分治法思想-棋盘覆盖//tr表示左上角行数，tc表示左上角列数，dr，dc表示特殊行特殊列，size表示规格void ChessBoard(int tr,int tc,int dr,int dc,int size){if (size==1) return;int t = tile++;int s = size/2;//1.覆盖左上角棋盘if (dr<tr+s && dc<tc+s)//特殊方格在这个棋盘中ChessBoard(tr,tc,dr,dc,s);else//此棋盘中无特殊方格,将特殊方格放在右下角{Brand[tr+s-1][tc+s-1]=t;ChessBoard(tr,tc,tr+s-1,tc+s-1,s);//覆盖其余}//2.覆盖右上角棋盘if(dr<tr+s && dc>=tc+s)//特殊方格在这个棋盘中ChessBoard(tr,tc+s,dr,dc,s);else//特殊方格不在该棋盘中,将特殊方格填充在左下角{Brand[tr+s-1][tc+s]=t;ChessBoard(tr,tc+s,tr+s-1,tc+s,s);//覆盖其余}//3.覆盖左下角棋盘if (dr>=tr+s && dc<tc+s)//特殊方格在这个棋盘中ChessBoard(tr+s,tc,dr,dc,s);else//特殊方格不在该棋盘中，将特殊方格填充在右上角{Brand[tr+s][tc+s-1]=t;ChessBoard(tr+s,tc,tr+s,tc+s-1,s);//覆盖其余}//4.覆盖右下角棋盘if (dr>=tr+s && dc>=tc+s)//特殊方格在这个棋盘中ChessBoard(tr+s,tc+s,dr,dc,s);else//特殊方格不在该棋盘中，将特殊方格填充在左上角{Brand[tr+s][tc+s]=t;ChessBoard(tr+s,tc+s,tr+s,tc+s,s);//覆盖其余}}int main(){ChessBoard(0,0,0,3,MAX_SIZE);for (int i=0;i<MAX_SIZE;i++){for (int j=0;j<MAX_SIZE;j++)cout<<Brand[i][j]<<'\t';cout<<endl;}return 0;}

结果截图：

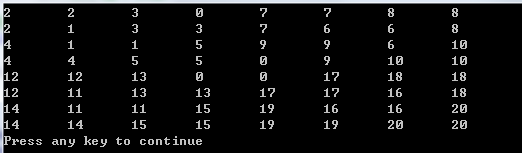
3.循环赛日程表

问题描述：设有n=2^k(k>=1)个选手参加网球循环赛，循环赛共进行n-1天，每位选手要与其他n-1位选手比赛一场，且每位选手每天必须比赛一场，不能轮空。试按此要求为比赛安排日程。

解法：

#include <iostream>using namespace std;#define N 64void GameTable(int k,int a[][N]){//n=2^k(k>=1)个选手参加比赛，数组下标从1开始int n=2;//k=1,可直接求出//求解两个选手比赛日，得到左上角元素a[1][1]=1;a[1][2]=2;a[2][1]=2;a[2][2]=1;int i,j,t;for (t=1;t<k;t++)//迭代处理，依次处理2^2,...2^k个选手比赛日程{int temp=n;n*=2;//填左下角元素for (i=temp+1;i<=n;i++)for (j=1;j<=temp;j++)//左下角元素和左上角元素的对应关系a[i][j]=a[i-temp][j]+temp;//将左下角元素抄到右上角for (i=1;i<=temp;i++)for (j=temp+1;j<=n;j++)a[i][j]=a[i+temp][(j+temp)%n];//将左上角元素抄到右下角for (i=temp+1;i<=n;i++)for (j=temp+1;j<=n;j++)a[i][j]=a[i-temp][j-temp];}cout<<"运动员编号\t";for (i=1;i<n;i++){cout<<"第"<<i<<"天\t";}cout<<endl;for (i=1;i<=n;i++){cout<<i<<"号运动员:\t";for (j=2;j<=n;j++)cout<<a[i][j]<<'\t';if (j==n)cout<<n;cout<<endl;}}void main(){int a[N][N];int k;cout<<"输入选手个数的次数：";cin>>k;GameTable(k,a);}

?结果截图：

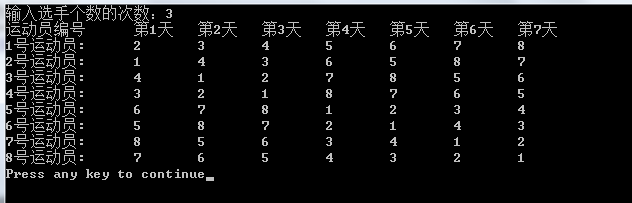
4.二分搜索

描述：将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

解法：

#include <iostream>using namespace std;//第一个参数表示有序数组，n表示数组元素个数，key表示需要寻找的数字int BinarySearch(int a[],int n,int key){int low=0,high=n-1;while (low<=high){int mid=(low+high)/2;if (key==a[mid]) return mid;if (key>a[mid]) low=mid+1;else high=mid-1;}return -1;}int main(){int a[]={1,3,5,8,22,45,65,78,102};cout<<BinarySearch(a,9,65)<<endl;return 0;}

?结果截图：

5.快速排序

算法思想见图：

程序描述：

#include <iostream>using namespace std;//求出“基准”所在的位置int patition(int arr[],int low,int high){int key=arr[low],i=low,j=high;//key保存初始基准位置if (low<high)while (i<j){while (i<j && arr[j]>=key) j--;//没有需要移动的数if (i<j)//存在需要移动的数{arr[i]=arr[j];i++;//i处数据已定，不需比较，故i++}while (i<j && arr[i]<=key) i++;if (i<j){arr[j]=arr[i];j--;}}arr[i]=key;//此时i==jreturn i;}void QuickSort(int arr[],int low,int high){if (low<high){int mid=patition(arr,low,high);QuickSort(arr,low,mid-1);QuickSort(arr,mid+1,high);}}int main(){int arr[]={2,3,4,1,3,45,23,12,43};cout<<"排序前：";for (int i=0;i<9;i++){cout<<arr[i]<<'\t';}cout<<endl<<"排序后：";QuickSort(arr,0,8);for (i=0;i<9;i++){cout<<arr[i]<<'\t';}cout<<endl;return 0;}

?6.归并排序

思想描述图示：

程序描述：

#include <iostream>using namespace std;//归并排序示例程序--从小到大void merge(int array[],int p,int q,int r){int i,begin1,end1,begin2,end2;//申请空间，空间大小为两个已排序列int *temp = new int[r-p+1];begin1=p;end1=q;begin2=q+1;end2=r;i=0;while ((begin1<=end1)&&(begin2<=end2)){//将有序的元素进行比较if (array[begin1]<array[begin2])temp[i++]=array[begin1++];elsetemp[i++]=array[begin2++];}while (begin1<=end1)//此时若前面的序列还有数字，全部附到temp的后面temp[i++]=array[begin1++];while (begin2<=end2)//此时若后面的序列还有数字，也全部附到temp的后面temp[i++]=array[begin2++];for (int k = 0;k<r-p+1;k++)array[p+k]=temp[k];delete []temp;}void merge_sort(int array[],int first,int last){int mid=0;if (first<last){mid = (first+last)/2;merge_sort(array,first,mid);merge_sort(array,mid+1,last);merge(array,first,mid,last);}}int main(){int array[]={1,5,2,6,3};for (int i=0;i<5;i++){cout<<array[i]<<"\t";}cout<<endl;merge_sort(array,0,5);for (i=0;i<5;i++){cout<<array[i]<<"\t";}cout<<endl;return 0;}

?

?

?

?

?

?

?

?

?

?