组合数学——polya定理及其应用

??? Polya定理

??? 设有n个对象，G是这n个对象上的置换群，用m种颜色涂染这n个对象，每个对象涂染一种颜色，问有多少种染色方案？一种染色方案在群G的作用下变为另一种方案，则这两种方案当作是一种方案。

??? 方案数为

?

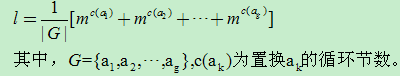
POJ2409

?? 题意：一家项链公司生产手镯。n颗珠子形成一个环，用m种颜色给n颗珠子染色，就得到了各种各样的手镯。但是，经过旋转和翻转使之吻合的算同一种方案。

例如，当用2种颜色对5颗珠子进行染色的方案数为8，如下图所示。

?

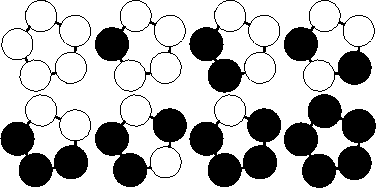
解：显然，对于这n个对象，有n种旋转和n种翻转。

1. 对于旋转，有c(gi) = gcd(n,i)，i为转动几颗珠子。

2. 对于翻转，当n为奇数时，c(gi) = n/2+1；

?????????????????? 当n为偶数时，有n/2个的循环节数为n/2+1，有n/2个的循环节数为n/2。

#include <iostream>#include <cstdio>#include <cstring>#include <cmath>using namespace std;typedef __int64 int64;int gcd(int a, int b){    return b==0?a:gcd(b,a%b);}//用m种颜色涂均匀分布在圆环上的n颗珠子的方案数int64 polya_circle(double m, int n){    int64 result = 0;    //旋转    for(int i = 1; i <= n; i++)        result += pow(m,gcd(n,i));    //翻转    if(n%2)        result += n*pow(m,n/2+1);    else        result += (pow(m,n/2)+pow(m,n/2+1))*n/2;    return result/n/2;}int main(){    int c,s;    while(true)    {        scanf("%d %d",&c,&s);        if(c==0&&s==0)            break;        printf("%I64d\n",polya_circle(c,s));    }    return 0;}

?

?

?