算法学习之数据结构之红黑树（一）
　　一，红黑树性质。

　　由于二叉查找树知道，一个高度为h的二叉查找树可以实现任何一种基本的动态几何操作，如search，insert，minimum，delete，successor等操作，其时间都是O(h)，这样树的高度低了就会执行的比较快，但是当树的高度较高时，操作的性能可能不比链表好。红黑树是许多“平衡的”查找树中的一种，他能保证在最坏的情况下，基本的动态集合操作的时间为O(lgn)。

　　红黑树的性质。红黑树是一种二叉查找树，，每一个节点增加一个存储位表示节点的颜色，为红色或者黑色。红黑树确保没有一条路径会比其他路径长出两倍。因而是接近平衡的。　　树的每个节点包含五个域：color, parent, key, left, right。一个二查找树如果满足如下红黑性质，则为一个红黑树。　　1)每个节点或是红的，或是黑的。 　　2)根节点是黑。　　3)每个叶节点（NIL）是黑的。　　4)如果一个节点是红的， 则它的两个孩子都是黑的。　　5)对每个节点，从该节点到其子孙节点的所有路径上包含相同数目的黑节点。　　从某个节点x出发到达一个叶节点的任意一条路径上，黑色节点的个数成为该节点x的黑高度。　　一个有n个内节点的红黑树的高度至多为2lg(n+1)　　　　二、红黑树旋转。　　当对红黑树上进行insert和delete时，对树进行了修改，结果可能会违反红黑树的性质，所以需要改变树中的节点的颜色和指针结构，即需要进行旋转。　　左旋，假设它的右孩子节点y不是nil[T]；x可以为树内任意右孩子不是nil[T]的节点，左旋以x和y之间的链为轴进行，它使y成为该子树新的根，x成为y的左孩子节点，而y的左孩子节点为x的右孩子。　　伪代码如下：

第一种：Z的“叔父”节点是红色。
 
              
 
如上图所示，在这种情况下，将父、叔节点都着为黑色，再将子树根节点着为红色，那么子树的黑高度没有发生改变，而且红黑性质得得到了调整。此时，再将Z指向子树的根节点，向上递归恢复红黑特性。
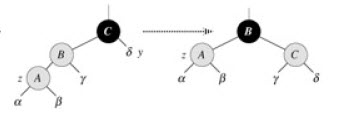
第二种：Z的“叔父”节点是黑色的，Z的父节点的右子节点。 
 
如上图，将Z本身与其父节点进行一次左旋，让Z指向原来的父节点，就可以调整为情况三，下面看情况三。
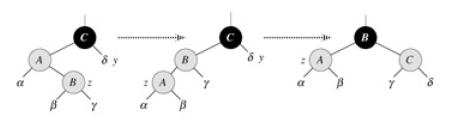
第三种：Z的“叔父”节点是黑色的，Z的父节点的左子节点。
 
如上图，将Z的父节点与祖节点进行一次右旋，并把父节点着黑色，原来的祖节点着红色。这些子树的红黑特性得到了恢复，而且子树的黑高度没有变化。另外，由于子树根节点已经是黑色了（这个节点不会出现父子同为红色的问题了），所以不必再向上递归了，此时整个树的红黑特性都已经是正确的了。
由于红黑树的删除比较复杂，放在下一篇。
网上发现不错的学习资料，分享一下：红黑树算法的层层剖析与逐步实现