Algorithms 第四版 习题 4.1.36 边连通性

4.1.36 Edge Connectivity 边连通性

定义：桥是如果从图中删去将生成两个子图的边。如果图中没有桥，则说该图是具有边连通性的。

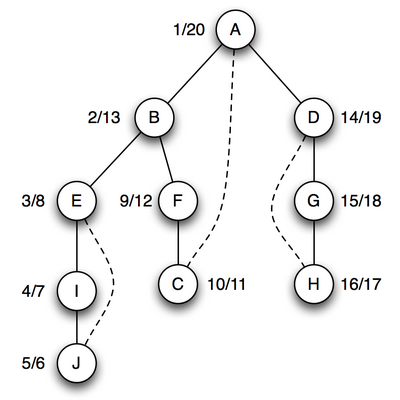
图片源：http://moodle.bracu.ac.bd/mod/page/view.php?id=465

如上图，通过深度优先搜索DFS得到的一颗DFS 树。对任意子树的根，如B，要连通他的孩子们时，除了通过DFS生成的Tree edge，树边，还可以通过指向

B自己或者其祖先（这里只有A）的back edge，反向边；如果反向边不存在，那么一旦切断Tree edge，它就不能和（部分）孩子们连通了。这条Tree edge就是桥。

这里，对于B，它与以E为根的子树不是边连通的，因为BE是桥；它与以F为根的子树是边连通的，因为这颗子树存在反向边（指向B的父亲A）。

同理可知AD也是桥。

于是，判断图的边连通性只需要知道 每一个点 V 及 点V 的孩子们是否有反向边，这些反向边是否指向 点 V 或者 点V 的祖先 即可：

1. 用数组保存DFS对点的访问顺序。

2. 用数组保存反向边信息，这些信息在每层DFS会更新；在下层DFS返回后，判断当前点V 的访问顺序 是否小于 V孩子们的反向边指向的最远祖先，

是则表明 点V 到该 最远祖先之间不存在桥（因为总有反向边）；否则说明 V与它孩子的 tree edge就是桥。

如果要输出所有桥，时间复杂度就等于 O(DFS) = O ( |V| + |E| )；只需判断边连通性的话在找到一座桥时返回就可以了。

测试数据：

0: 6 2 1 5
1: 0
2: 0
3: 5 4
4: 5 6 3
5: 3 4 0
6: 0 4
7: 8
8: 7
9: 11 10 12
10: 9
11: 9 12
12: 11 9

DFS结果是包含3棵树的树林

代码如下：

package com.cupid.algorithm.graph.algorithms4th;import java.io.File;import java.io.FileNotFoundException;import java.util.Scanner;// Algorithms 4th ed. 4.1.36// Definition:// A bridge in a graph is an edge that, if removed, would separate// a connected graph into two disjoint subgraphs. A graph that has no bridges is said// to be edge connected.2public class EdgeConnectivity {// The number of visit to each vertex during DFS.private int[] dfsOrder;// For any Vertex v, whichAncestor[v] tells that the farthest ancestor it can reach via its own or its children's back edge.// If no back edge, it means it can only connect to parent through a DFS Tree edge.private int[] whichAncestor;private int count;private Graph myGraph;private boolean noBridges = true;public EdgeConnectivity(Graph G){this.myGraph = G;count = 0;dfsOrder = new int[G.V()];whichAncestor = new int[G.V()];for(int i=0;i<dfsOrder.length;i++){dfsOrder[i] = 0;}}private void DepthFirstSearch(){for(int i=0;i<myGraph.V();i++)if(dfsOrder[i] == 0){dfs(i,i);}}private void dfs(int u,int predecessor){count = count + 1;dfsOrder[u] = count;// By default, no back edge connecting vertex u and any ancestorwhichAncestor[u] = count;for(Integer v: myGraph.adj(u)){// If adjacent vertex has not been visited...if(dfsOrder[v] == 0){dfs(v,u);// When the next level of DFS returns,// Update back edge information.if(dfsOrder[u] >= whichAncestor[v]){whichAncestor[u]  = whichAncestor[v];// If, for vertex u, there is no back edge connecting its ancestors,// A bridge exists, connecting u and its child, v.}else{noBridges = false;System.out.println("A bridge is found:" + u + "-" + v);}// When dfsOrder[v] > 0, a back edge is found.// Because there may be many back edges,// we should update back edge information as the one to the farthest ancestor.}else if(dfsOrder[v] > 0 && v!=predecessor){if(dfsOrder[v] < whichAncestor[u])whichAncestor[u] = dfsOrder[v];}}}public boolean isEdgeConnected(){DepthFirstSearch();return this.noBridges;}public static void main(String[] args) {File file = new File("d:\\tinyG.txt");try {Scanner in = new Scanner(file);Graph G = new Graph(in);System.out.println(G);EdgeConnectivity ec = new EdgeConnectivity(G);System.out.println("\nIs the graph edge connected ? " + ec.isEdgeConnected());}catch(FileNotFoundException e){e.printStackTrace();}}}

另外，与桥紧密相关的概念是 关节结点，可参考：http://www.csie.ntnu.edu.tw/~u91029/Connectivity.html