【中国剩余定理】POJ 1006 生理周期
http://poj.org/problem?id=1006&lang=zh-CN&change=true

Sample Input
0 0 0 0
0 0 0 100
5 20 34 325
4 5 6 7
283 102 23 320
203 301 203 40
-1 -1 -1 -1

Sample Output
Case 1: the next triple peak occurs in 21252 days.
Case 2: the next triple peak occurs in 21152 days.
Case 3: the next triple peak occurs in 19575 days.
Case 4: the next triple peak occurs in 16994 days.
Case 5: the next triple peak occurs in 8910 days.
Case 6: the next triple peak occurs in 10789 days.

中国剩余定理【孙子定理】详解：

其实就是解方程组：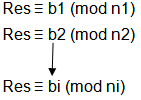

求res的值
使用中国剩余定理的条件【重要！！！】：
n1，n2，n3……ni 这些数两两互质(互素)！！也就是两两之间的最大公约数是1！！

回到正题：先看一下这个视频，后面的会更好理解！
http://v.youku.com/v_show/id_XMTExNTAzOTIw.html

算法描述：【利用同余的加性和乘性】
令nn = n1×n2×n3×……×ni;
那么也就是说nn是ni的倍数！
所以有：nn/ni是其他n的倍数，不是ni的倍数，而且nn/ni跟ni没有大于1的公约数
【如nn/n2，是n1,n3,n4...的倍数，但不是n2的倍数，而且nn/n2和n2的最大公约数是1，因为上面说了这些数两两互质】
既然nn/ni是其他n的倍数，那么nn/ni这个数模其他n【n1,n2...n[i-1],n[i+1]...】的结果肯定是0，为下面利用同余的加性奠定了基础

所以根据视频那种方法
可以先找到x使得：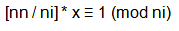

假设找到这个x了，那么要满足第i个方程，则利用同余的乘性必有：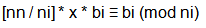

那么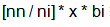就是res的一部分，它使得res满足第i个方程
所以利用同余的加性，把满足所有方程的这么一个部分加起来就是求出来的其中一组解了

怎么找x呢？【关键】
∵有重要条件：两两互质
∴nn/ni和ni也互质
∴【根据上述:使用中国剩余定理的条件】
∴由扩展的【欧几里得】得：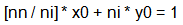

∴两边同时模ni得：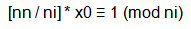

跟上面的式子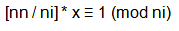对比，发现x = x0
x0怎么求？
不就是利用【扩展欧几里得定理】咯！


另外推荐题目：http://acm.hdu.edu.cn/showproblem.php?pid=1930

#include <iostream>#include <fstream>#include <algorithm>#include <string>#include <set>//#include <map>#include <queue>#include <utility>#include <iomanip>#include <stack>#include <list>#include <vector>#include <cstdio>#include <cstdlib>#include <cstring>#include <cmath>#include <ctime>#include <ctype.h>using namespace std;void Egcd (int a, int b, int &x, int &y)    //扩展欧几里得【无返回版】求x{if (b == 0){x = 1, y = 0;return ;}Egcd (b, a%b, x, y);int tp = x;x = y;y = tp - a/b*y;}int CRT (int n[], int b[], int nn){int res = 0, x, y, i;for (i = 0; i < 3; i++){int a = nn / n[i];Egcd (a, n[i], x, y);    //求xres += a * x * b[i];    //把所有组成部分加起来【加性】}        //其中*b[i]是利用了同余的乘性return res;}int main(){int n[5] = {23, 28, 33}, b[5], i, date, k = 1, x0;while (1){for (i = 0; i < 3; i++)scanf ("%d", b+i);scanf ("%d", &date);if (date == -1)break;x0 = (CRT (n, b, 21252) - date) % 21252; //使解不大于21252if (x0 <= 0)x0 += 21252;  //负数或0特殊考虑printf ("Case %d: the next triple peak occurs in %d days.\n", k++, x0);}return 0;}