线性判别函数(一)

又是礼拜天了，嗯，线性函数这块今天起个头，争取能写完。

与之前讲的不同，线性判别函数中，我们对样本的信息知道的很少（比如，我们不知道样本的概率分布），但对于给定的样本集，我们知道其所属的类别。我们现在希望用一个线性函数作为判断的边界，将两类样本区分开来。如下图所示：

在我们假设在图中两类样本是线性可分的情况下（不可分的情况，我们可以通过核函数将其映射到高维），我们需要知道上图线性函数的参数。

采用线性判别函数，主要基于两点考虑：

1.很简单的模型

2.易于计算

线性判别函数可以写成如下形式

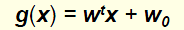
其中w0叫做阈值权（threshold）或者偏置（bias）

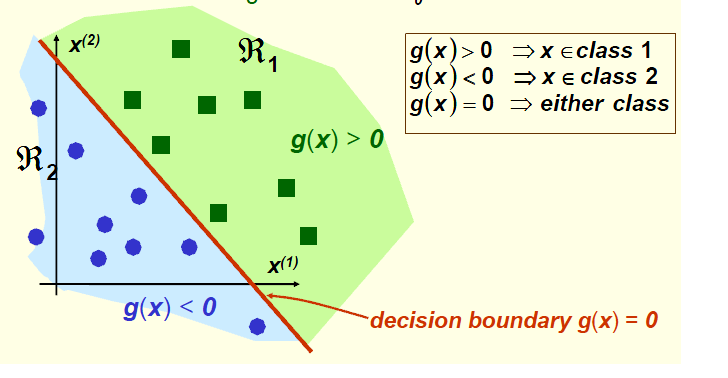
决策边界是一个超平面

1.在一维的情况下，决策边界是一个点

2.在二维的情况下，决策边界是一条线

3.在三维的情况下，决策边界是一个面

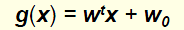
w决定了决策边界这个超平面的方向

w0决定了决策面的位置

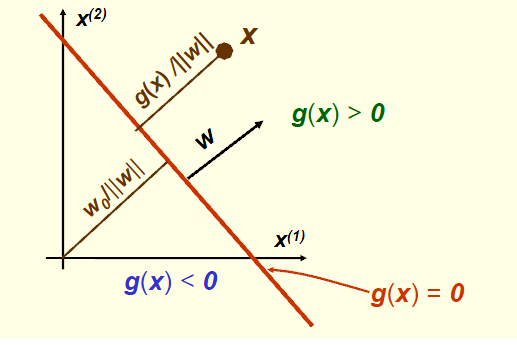
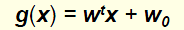
我们将其改写为

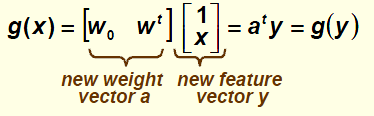
y我们称之为增广特征向量

在x向量的第一维增加一个1，我们将问题转变了

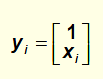
此时决策边界如下图所示：

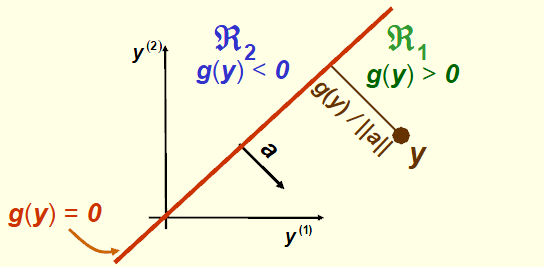
我们的目标就是找出线性判别函数的权值a

在我们的决策边界没有误差时，我们有：

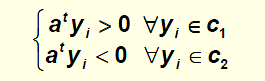
我们可以将其转换为：

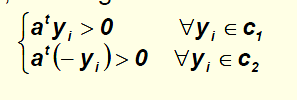
上式的意思即为：对所有属于c2类别的样本，我们使用-yi代替yi

然后我们在寻找权重向量a，使得

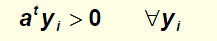
如果原来的样本是线性可分的，我们一定可以找到满足条件的a

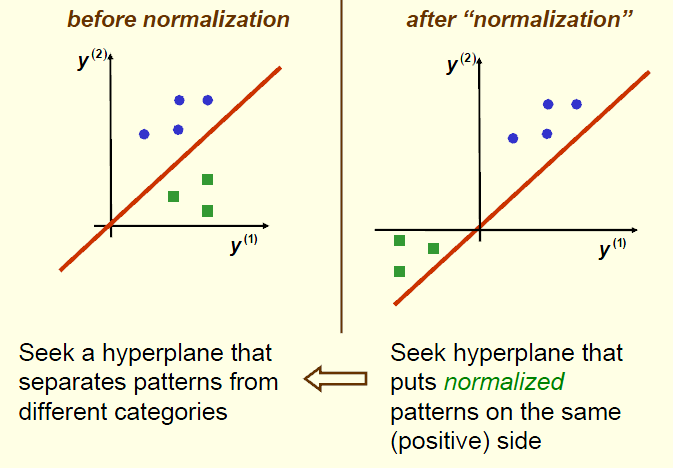
定义什么的就先介绍到这，具体如何求解a，我会在以后的博文中介绍