C语言名题精选百则——排序

?

?

第5章排 序问题5.1 二分插入法（BINSERT.C )插入式排列法（Insertion Sort)是一个极为简单的方法，但它的效率却很低，因为比较
次数与n2成正比，n是数据个数；而且还有大量移动数据的操作。编写一个程序，在这两 点上作一些改进，使得比较次数与nlog2n成正比，而且移动数据的速度加快。
【说明】

插入法是可以加快的。第一，如何把数据插到已排好的一串数据中；第二，移 动的动作也可以加快。改进之后，也许它仍然不能与快速排列法等相提并论，但快3?4倍 总不是难事，知道要如何编写吗？
提示：留心一下二分查找法与C语言中的<string.h>标准链接库函数。
问题 5.2 Shell 法（SHELL.C )在传统的教科书中，Shell排列法都是直接引用D.L.Sheil当年原著中的办法，在要排序的数组中，先把间隔为n/2的元素排好，然后把间隔为n/4的元素排好，再排间隔为 n/8,n/16,…,4,2,1的元素，最后就是一个依顺序排列完成的结果。D.Knuth曾经在他的著 作中证明，Shell方法要用与n^1.5成正比的比较次数（当然已经比插入法等快了一些)，不过 最近Sedgewick等人却找出了更快的办法，证明可以把Shell方法加快到只用到n^4/3成正比的比较次数。试编写一个程序，找出一组更快的方法。
【说明】
D.Knuth很早就知道如何用3^i-1)/2的方式，亦即1，4，13，…，这样的方法会比Shell 原来的做法好一些。换言之，如果有n个元素，就得找出满足(3^i-1)/2<n的最大一个i 值，大约是[log2(2n-1)/log2 3]。找到了 i之后，就排间隔为(3^i-1)/2的元素，再排间隔为 (3^i-1)/2的元素，…，最后排间隔为13，4，1的元素等。这种方法会比较快，有其直观的
意义，因为若间隔为n/2，n/4,n/8，…时，就会有很多重复的比较。例如，，以n = 8为例， 第一次会比较x[0]与x[8]，第二次间隔为4时会比较x[0]，x[4]，x[8]，但x[0]与x[8]早就比较过，同理第三次间隔为2,比较x[0]，x[2]，x[4]，x[6]，x[8],不就有更多重复的比较了吗？而 这些重复了的比较数的结果在此之前就已经知道了，因而Knuth提出的间隔节省了时间。
近年来，Sedgewick研究过快速排列法之后，再接再厉研究Shell排列法，也得到一些重要的成果，建议把间隔定为下式：
4^(j+1) + 32j +1
于是Shell方法的速度就可以降低到只用与n^4/3成正比的比较次数而己，这又比n^1.5进 了一层，虽然1.5只比1.33多不了许多，但理论家却是相当兴奋的。
请用上述Sedgewick的方法来编写程序。
问题5.3快速排列法（QSORT.C )读者可以找一本书，研究一下快速排列法（Quicksort)的概念，并且写成程序。
【说明】
快速排列法是C.A.R.Hoare提出来的方法，它需用到递归的技巧。它的概念是这样的,
有一个数组x[],它有n个元素。如果能够在x[]中找出一个元素x[k]，使得在x[k]左边
都比x[k]小或相等，在x[k]右边的则大于或等于x[k]:
截图

?因此，只要把x[1]?x[k-l], x[k+1]?x[n]分别排列好，两者合并，就可以把整个x[]排好了。所以为x[1，…，n]排序就分成两个部分，第一部分是找出一个分界点x[k]，满足上述的 第二部分是递归地去排x[1,…,k-1]与x[k+1,…,n]，排好后结果就出来了。所有快速排列法程序的差异都在第一步——如何找出分界点x[k]。问题5.4保持等值的原来顺序（QSORT_L.C )快速排列法（Quicksort)有一个缺点，就是相等的数据在排序完成后不会保持原来的 顺序。不过，这个问题不难克服，使用连接串行的（LinkedList)技巧就可以容易地克服它; 编写一个程序完成这项工作。
【说明】
快速排列法虽然在一般情况下表现极为出色，却也有许多缺点，如果这些缺点不能一 一克服，那么速度再快也是枉然,在这个问题中本书打算提出一个快速排列法不稳定(Unstable)的问题。所谓的一个稳定的排序方法，不但要能够把数据的大小顺序排好，而 且还得维持在输入数据中值相等的各个数据的顺序。这一点看起来不重要，因为在书本上 只排整数、实数或字符串而已，但在实际的应用中，却常常排一个文件的记录，这就可能 会出问题了。就以电话簿为例，如果每一个记录都包含了姓名、电话号码、‘地址这3项数 据，而希望只依姓名顺序排列，当然同名同姓的人不在少数，如果再按姓名排列时不能依 输入顺序来处理同名同姓的人，那么在使用这个文件时就有可能出现问题。例如，本来John Smith在第100号记录，在查询时就希望他出现在那，但一经排列，这个数据很可能就脱离 原有的位置，而当姓名栏相同时的顺序规则，使用起来不就是很不方便吗？
要维持值相同的数据的顺序并不十分难，这会在习题中讨论，不过却会引入很多额外 的工作。不过，如果用串行来处理，那么这个问题就简单了。在程序中不妨假设输入是一 个串行，在“分”的时候就把输入串行分成3个部分串行，分别连接那些小于、等于、大 于某个值的元素，再递归调用自己去除小于、大于这两部分，排好之后，把小于、等于、 大于这3个子串行再串回来，不就得到一个排列完成的串行了吗？如果在“分”的时候注 意到加入“等于”那个串行中的顺序与输入的顺序相同，那么快速排列法就是一个稳定 (Stable)的排序方法了。
问题5.5非递归、无堆栈快速排列法（QS0RTJ.C)许多人都批评快速排列法，但是观点却集中在快速排列法使用了递归的方法；事实上 这一类的批评虽然并不完全是有的放矢，但是却不曾切中要害，换句话说，这并不是快速 排列法的最严重缺点。无论如何，写一个不用递归的快速排列法却可以让不少人安心，请 问能不能写一个不用递归，但也不用堆栈的快速排列法来排正整数呢？
【说明】不用递归很简单，用数组作堆栈来仿真递归的动作即可。下面是几点有用的建议。首
先，把问题集中在只排正整数上头，换句话说，输入数据全是正值，因此负的数就可以在
数组中作记号用。
仔细回想在快速排列法中用Lomuto方法把原数组分解成两部分时的方法，一旦数组
分解完了，中间的基准元素就明确了位置；换言之，它算是已经排好了。这是一个非常重
要的方法，因此往后的工作中就不必处理这个元素。为了方便起见，把这个变量存回数组， 往后凡是碰到负值的数，就表示是已经排好了的。
递归方法此时分成两次使用，一次做左半，一次做右半。不过本书不打算用递归，过
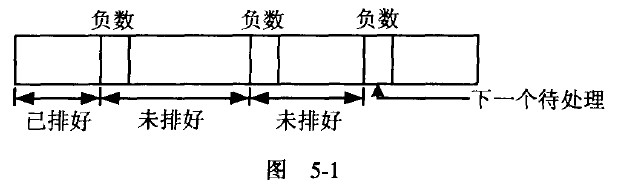
程就要-杂些。读者不妨这样想，再加一个指标，指向被排好的元素，或是己排好部分的
下一个元素，如图5-1所示。
因此，可以不断地分割，直到x[0]排好为止；然后向前移，再分割，直到x[l]排好，…， 最后使x[n-1]也排好，工作就完成了。不过应注意一点，就算x[0]好了，这不单是x[0]被排好，往往在x[1]?x[n-1]之间也有不少元素被排好了。截图

?问题5.6求中位数（MEDIAN1.C )中位数（Median)是将一组数从小到大排好后居中的数；如果这一组数的个数为奇数, 那么中位数是存在的；但若个数为偶数，就没有中间的那一个数了，因此取居中两个数的 平均数。例如，3，1，7，5，9经过排列后是1，3，5，7，9，所以中位数是5;但3，1，7,5，9，4,经过排 列得到1，3，4，5，7,9，所以中位数就是(4+5)/2=4。为了方便用整数计算，编写一个程序，接收 一个整数数组，不必排大小而找出该数组的中位数。
【说明】
只要一排好大小，问题就简单了，所以规定不能排大小。求中位数的方法很多，有些 方法中看不中用，也就是说理论上很快，但程序不太好写。不过，倒是有一个现成的方法 可以用,虽然效率不是很高。这个题目的提示是，何不仔细研究一下快速排列法中叫做split() 的程序与快速排列法的内涵呢？仔细想想就可以得到一个不错的方法。
问题5.7堆积法（HEAPSORT.C )编写一个堆积排列法（Heap Sort)的程序。读者可以参考身边任何参考书，但注意一 点，程序尽量编写得有效率。
【说明】


这就是堆积法的大概，编程时要注意以下几点：
(1)没有必要用树状结构，用数组就行了，若要达到这一点，要了解每一个元素在数 组中的相对位置；有一个简单的办法是这样的：把顶点元素放在数组第一个位置，它的两 个后代放在第二、第三个位置，然后就从上到下、从左到右地排下去。那么x[i]的后代在 什么地方呢？
(2)也没有必要用额外的数组来存放排好顺序的元素，事实上可以在原地完成工作。
(3)建议编写一个名为fix_heap()的函数，用来接收一个元素，把该元素以下的部分 还原成堆积；然后就可以通过这个函数来排序了。
(4)注意C语言的数组脚码从0开始的事实，在处理上有没有什么困难？
问题5.8改良的堆积法（HEAP_NEW.C )在用堆积法排顺序时会有一个很明显的缺点，许多优秀的程序员或许都能看出来。如 果现在要决定x[i]是不是应该在目前的位置，需要找出在堆积中x[i]的x[2i]与x[2i+l], 再用这两者中大的一个（用一次比较）与x[i]相比（第二个比较)，如果x[i]比较大，问题 就解决了；但若x[i]比较小，就得把x[2xi]与x[2xi+l]中大的那一个与x[i]互换，再去处 理在新位置的x[i]值。很明显地，把一个值每往下移一层就要两次比较，是不是太多了一 些？请运用一项技巧来克服这一短处。
【说明】
如图5-14所示，它是一个堆积的某部分。在箭头所指的地方的元素不满足堆积的条件， 所以找它的后代（98, 81)与大的那个比，于是两次比较把98放到上方空位；下来再找原 98所在地的后代，大的一个是80,与50比较，比50大，所以再两次比较把80送到原98 所在的地方；第三步，用原80所在地的后代中大的一个与50比，即70与50比，因此把70 送到原80的所在地；最后拿原70所在的两个后代中大的那一个55与50比，还是比50大， 所以把55移到原70所在，而由50占据55的位置，一共用了 8次比较，是不是太多了呢？截图

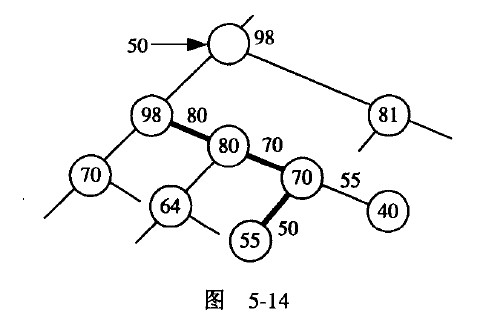
?提示：仔细看看在比较过程中所经过的路径，它有什么特色？父与子的关系如何？突破这一点，编写的程序也不一定比原来的fix_heap()长。
问题5.9合法（M_SORT.C )
合并排列法（Merge Sort)是把要排序的数据分成大约相等的两组，把这两组的顺序排 好之后，通过合并的方法而合成一个全部都排好的结果。编写一个程序实现这个想法。
【说明】
这是一个很标准的分而治之—ivide and Conquer)方法的运用，假设要排序的n个数 据是放在一个数组中，如图5-15所示。截图

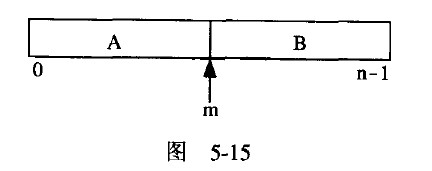
?把它分成均等的两段，即A与B,这是分的动作；接着以递归的形式把这两段排好， 这是治的动作；最后，当这两部分都排好了，使用合并（Merge)的方法就可以重新合成一 个全部排列完成的数组，这正是合的动作。
有了这种方法，能否写出一个又简洁又有效率的程序呢？
问题5.10捅子法（BUCKET.C )快速排列法（Quicksort)、二分插入法（Binary Insertion Sort)、堆积法（Heap Sort)， 合并法（Merge Sort)等，都至少要用与nlog2n成正比的比较次数来排n个数据（当然，
不一定是数值)。但如果要排的不过是一群正整数（unsigned int),有没有更快的方法？请 写出这个特殊排序的程序，目的是打破nlog2n的限制。
【说明】
在一些数据结构或算法的书中都会提到，任何一个“一般性”的排序方法都至少要用 与nlog2n成正比的比较次数。但是在实际应用中，要排序的对象却往往是一连串的正整数,
因此似乎用不着“一般性”的方法才对，所以这个问题是有没有一个特殊的方法来排正整 数，不但如此，还要求更快，而且打破nlog2n的限制。心目中有这种方法吗？
注意：个方法上的问题，nlog2n这个值的来源，假设在排大小的时候只会用到比 较、移动兀素的操作，而不对被排列的数据作进一步的处理，因此理论家说，这就是“决策树模型”。不过现代的计算机的功能肯定不止比较、移动元素这两者，肯定还有其他 的功能，所以为了打破这一限制，就不能只用“决策树模型”，而要运用进一步的技 巧了。如果对数据处理一次，就认为对它作了一次比较，那么程序一共作了多少次“比 较”呢？
问题5.11单一重复元素排序（LOT_DUP_C )如果一个数组中有n个元素,但是并非每一个元素都不相同;事实上,只有大约alog2 n 个值是不同的，其余n-alog2n个值全部一样，请开发一个特别快的程序把数组的元素排 好顺序。（a是个常数，为了方便起见，可以当成1;另外，n-alog2n>0)，而且n比alog2n
大很多。请问程序用了多少次比较？
【说明】
如果n是16, log2n就是4，这个题目是说，在16个数中只有4个左右是不同的。下 面就是一个例子：
37334333
33393333
这16个数中只有3，4,7，9是不同的，其他都与这四者中之一相同。这是一个非常特殊 的排序题目，如果用快速排列法这些一般方法去排的话，就会很浪费时间，因为有太多相 同的元素在内。
理论上，任何一般用途的排序方法都至少要用与nlog2n成正比的比较次数，但是对这
个特殊问题而言，因为有太多相同的元素在内，往往只要与n成比例的比较次数就可以了， 有没有办法做到这一点？
问题5.12均匀重复元素排序（LOG_DUP.C)如果一个数组有n个元素，但却只有alog2n个不同的值，换句话说，数组中有alog2n 不同的值，每一个都重复出现了 n/(alog2n)次。编写一个特别快的程序把数组的元素排好 顺序。假设n很大，比alog2n大很多，a是个常数；试问程序用了多少次比较。为了方便
起见，可以把a当成1。
【说明】
课本中学到的大小排列方法，其实是一种极为一般性的，对任何类型数据都适用的
方法。但是对特殊的数据而言，这些一般性的方法就不见得有其长处了。什么是特殊数
据？例如几乎已经排好的数组、只在某个范围中的整数，或者是有很多重复的数据等。 己经看到过用Bucket法排正整数，或有log2nt数相异，其他完全相同的数组，都只需要大约与n成正比的比较次数就可以了。在本题中是另一个特殊的例子，在n个数据中 有log2n个不同值，这意味着在最坏的情况下，n个数据分成log2n组，每一组中的数据
完全相同；最好的情况则是除了这log2n值之外，剩下的n-log2n个值都相同。后者在问 题5.11中见过了，比较次数大概与n成正比，在这个问题中可以得出前者答案，因为前
者包含了后者。
这个题目用不着高深的数据结构，用本书中的方法，再加上一点灵巧的心思就可以做 出来。一般的排序方法都会用与nlog2n成正比的比较次数，读者应该试试写一个能够达到
与nlog2(log2 n)成正比的比较次数的程序。
提示：不能去排整个数组，应在合并（Merge )的动作上动动脑筋，另外，如果学过数据结 构，就应该看出有一个极为适用的结构。
问题5.13谁积式合（HEAPMERGC )已知m个数组，每一个数组都有n个元素；为了方便起见，这m个数组正好是x[][] 矩阵中的m列。如果这m列中的元素都各自以从小到大的顺序排好了，编写一个程序把这 m*n个元素合并到一个大矩阵中。不过在做这个题目时有进一步的限制，因为内存有限， 大概最多只有与m成正比的内存可以使用。请问如何克服这一层限制？当然，程序的速度 就会慢了。
【说明】
这个题目最简单的做法就是把矩阵两列两列地合并，因为每列有n个元素，合并n列 大约只要与mn成正比的比较次数，但内存却差不多要多出一倍，也就是2mn,而所想 克服的就是这一点，用时间来换取空间。
其实这个题目有它实用上的意义；如果把m个己排好顺序的数组想象成m个已经排列 好的文件，想把这m个文件合成一个更大的、排好顺序的文件时，两者对比就很容易明白 为什么要有那一层限制了。文件的长度是很大的，常常大到内存放不下，但文件的数目却 显然不会太多，因此限制就是能够用与文件数目成正比的内存来做这件事。
假设内存中可以储存10000个数，而有1000 000个存放在文件中的数要排列，就可
以把1 000000个数每次读10 000个，排好后放到一个文件中；再读接下来的10 000个数,
排好后放到第二个文件，因此共产生100个文件，下来用差不多与100成正比的内存就
可以把100个文件合并成一个排列完成的大文件了。当然，或许读者会想，100个文件多
不可思议。不过这没有问题，如果嫌100个太多，25个如何？可以把上面的步骤分4次完
成，在每一次都用25个文件，而合并成一个文件（内容为原文件的1/4);最后再做一次4 个文件的合并就可以得到结果。
当然，这并不是一个好的排序的建议，但事实上的确是一个可行的做法，笔者用过的 一些系统中就把这种方法在排序系统的某一环中运用过。读者能够想到一种方法来做这件事吗?
问题5.14裣数组元素是否相异（UNIQUE.C )
已知一个数组，编写一个程序把相同的元素去掉而只留下一个。
【说明】
这个问题几乎所有人都会做，简单极了，但正因为简单，就会常常不知不觉地接受常 见的、没有效率的做法而不自知。一般做法是：假设已经给定的数组x[]，元素有n个； 再令m是已经找到的全不相同的元素个数，开始时x[0]—定可以在数组中，所以m为0。
接着令i为1?n-1,对于每一个x[i]而言，看看它是否与x[0]，x[2]，…，x[m-l]这些元 素相同，如果不相同，那些相异的元素就又多了一个，因此令m为m+1,把x[i]放到这个 新的位置中;但若x[i]与某个在x[0]?x[m-l]的元素相同，那么x[i]就可以去掉了。所以 当全部n个元素都处理完后，x[0]?x[m]中就是那些相异的元素。
这种方法是正确的，但一共比较了多少次呢？在最坏的情况下，就是n个元素全不相 同，处理到x[i]时m的值为i-1, x[0]，x[1],…，x[i-l]都不一样，一共比较了i-1次。因此程 序令i从2变到m时，比较了 ：
1 + 2 +…+i-1+…+(n-1)=n(n-1)/2也就是近乎n2次。这是个比较慢的方法，有没有办法打破这个限制，写出更快的程序？
问题5.15数组中和为零的段落（ZEROSUM.C )已知一个整数数组，其中可能有正整数、负整数与0,而且元素也不会重复出现，编 写一个程序找出这个数组中是否有一个子数组元素的和为零。所谓的子数组，就是原来数 组中连续的若干（至少一）个元素。例如，如果数组为1,2,3，-5，4，那么2，3，-5这个子数组
中元素的和就是零。
【说明】
很多程序员的做法是：如果原来数组x门有n个元素，那么就准备一个nxn的矩阵 A = [aij]，其中aij储存了 x[i]?x[j]的和，换言之：
aij=x[i]+x[i+1]+…+x(j]，i<j
当把A =?[aij]算出来之后，再去查有没有值为零的元素；当然还有其他的做法，有的也
许不用4矩阵，但是还是在算aij。这样的做法要做n(n -1) / 2次比较,因为有n(n -1) / 2个aij，
亦即x[i]+…+x[j],效率是很差的，不但如此，还要多出额外的空间。对于这个问题而言， 程序应该做到比n(n -1) / 2还少的比较次数。
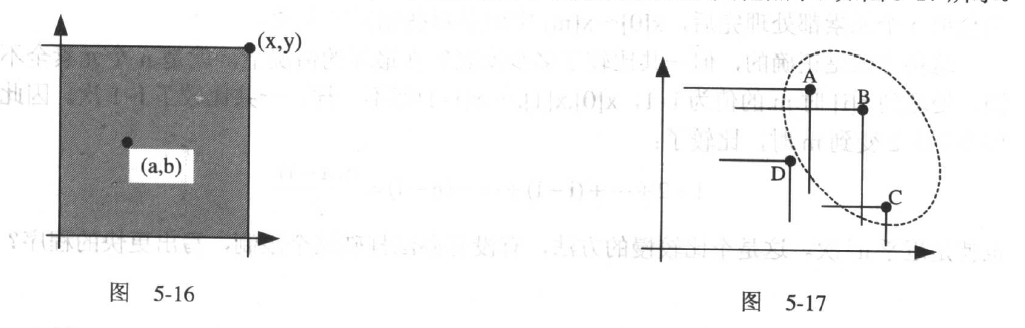
问题5.16平面上的极大点(MAXSET.C )在平面上如果有两个点(x，y)与(a，b)，说(x,y)支配—ominate) 了(a，b),这就是指 x≥a而且y≥b;用图来看就是(a，b)座落在以(x，y)为右上角的一个无限的区域中。对于平面上的 任意一个有限点集合而言，一定存在有若干个点，它们不会被集合中任何一个点所支配， 这些点构成一个所谓的极大集合。编写一个程序，读入一个点的集合（比如以(x，y)这样的 坐标形式），找出这个集合中的极大集合。如果(x，y)支配(a，b) , x≥a, y≥b ,那么(a，b)就在x的左方、y的下方，如图5-16
所示。
如果有n个点，那么就有可能某些点被支配，又有某些点支配其他点了，如图5-17所示。截图

?
在图5-17中，A支配D, B也支配D,但C却什么也没支配；不但如此，A，B，C都不
曾被任何点支配，所以极大集合就是{A，B，C}。
严格地说，程序是不难写的，可以先固定一个点(x，y),然后对于每一个不是(x，y)的 点(a，b)而言，检查(a，b)是否支配(x，y),如果是，（x,y)就不可能在极大集合中；所以当
每一个点都做过这一步骤之后，就知道哪些点不在极大集合里，当然其他的点就构成极大
集合。但是，这种方法比较慢，大约要用到与n2成正比的检查次数，所以要求使这个程序
快一些。在此有几点建议。第一，排大小有点用处；第二，在极大集合中的点的y坐标有什么 特性？如果能够多画几个图，很快就可以想出一个漂亮而且简单的方法。
问题5.17宴会中问数目的大埴（MAXVISIT.C)在一个宴会中一共有n位来宾，按照来宾的到达与离去的登记时间，知道第i位来宾 在Xi时到达，在Yi时离开，因此第i位来宾在宴会中的时间是[Xi，Yi],亦即Xi ? t? Yi中所有可能的t，编写一个程序，读入Xi与Yi，1≤i≤n，找出同一时刻之内最多会有多少人 同时在宴会场所中。
【说明】


问题5.18包含在其他区间中的区间（CONTAIN.C )
已知一组区间[ai,bi]，i=l,2,…,n；编写一个程序，找出这些区间中有哪一些会包含 在其他的某个区间中。
【说明】
为了处理问题的方便，不妨假设ai<bi，所有ai与bi都是整数，而且没有重复出现的
区间。如果有3个区间[0,2]、[2,4]、 [1,3],于是没有任何一个区间会包含在第一个区间之 内；但若区间是[1，3]、[0,2]、[2,3]、[3,4],于是[2，3]就包含在[1，3]之内，但[1，3]、[0,2], [3,4] 都不包含在任何一个区间中，如图5-18所示

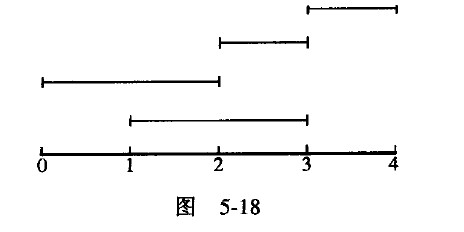
?这个题目看起来杂乱无章，但是事实上有一个很简单的解决方法。提示：何不仔细地研究一下上一个求最多访客的例呢？这个目的解法与问5.17的技 巧多少是有一些类似的。

?