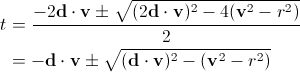光线追踪(RayTracing)算法理论与实践(一)入门
提要

本文先介绍光线追踪的理论,然后着重一步一步来搭建渲染场景,从最基本的向量类开始.采用的语言是c++,利用面向对象的思想,一些基础的线性代数和空间几何的知识也会用到，编程的框架用的是GLFW，渲染用到的是OpenGL。

光线追踪，简单地说，就是从摄影机的位置，通过影像平面上的像素位置(比较正确的说法是取样(sampling)位置)，发射一束光线到场景，求光线和几何图形间最近的交点，再求该交点的著色。如果该交点的材质是反射性的，可以在该交点向反射方向继续追踪。光线追踪除了容易支持一些全局光照效果外，亦不局限于三角形作为几何图形的单位。任何几何图形，能与一束光线计算交点(intersection point)，就能支持。

示意图如下:

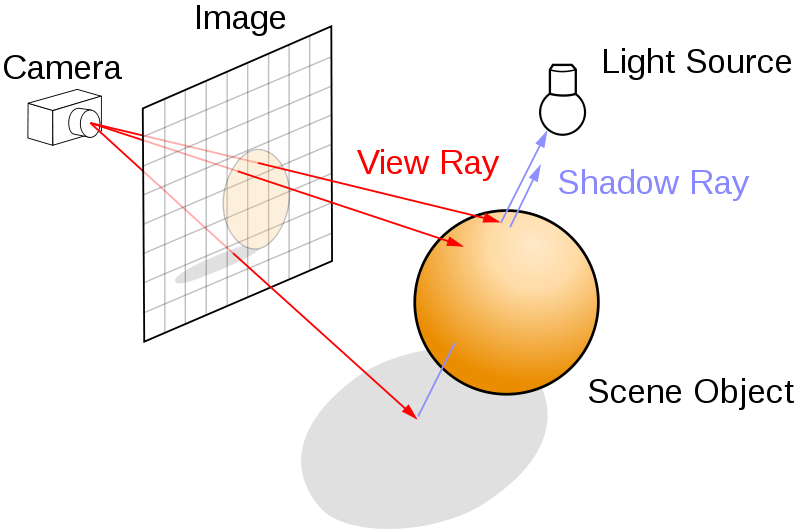
光线追踪有一些很棒的特性,比如:能够生成高度真实感的图形,特别是对于表面光滑的对象,缺点是所需的计算量大的惊人.

原理其实非常的简单,但具体实现起来的时候会有很多细节的地方.

代码实现

可以表示空上的点（x,y,z）.

gvector3.h

点乘，也叫向量的内积、数量积。顾名思义，求下来的结果是一个数。 在物理学中，已知力与位移求功，实际上就是求向量F与向量s的内积，即要用点乘。 

叉乘，也叫向量的外积、向量积。顾名思义，求下来的结果是一个向量，记这个向量为c。 向量c的方向与a,b所在的平面垂直，且方向要用“右手法则”判断（用右手的四指先表示向量a的方向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c的方向）。

在物理学中，已知力与力臂求力矩，就是向量的外积，即叉乘。 

数值上的计算，将向量用坐标表示（三维向量）， 若向量a=(a1,b1,c1)，向量b=(a2,b2,c2)， 则 向量a向量b=a1a2+b1b2+c1c2 向量a×向量b= | i j k| |a1 b1 c1| |a2 b2 c2| =(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1) （i、j、k分别为空间中相互垂直的三条坐标轴的单位向量）。

光线类有两个私有成员，原点和方向，数学上可用参数函数来表示：r(t)=o+td;t>=0cray.h

球体球面的几何定义是到空间某点距离一定的点的集合。
所以空间球体可以用两个参数来表示：圆心位置和半径。
代码如下。
csphere.h


若根号内为负数，即相交不发生。另外，由于这里只需要取最近的交点，因此正负号只需取负号。
摄像机
摄影机在光线追踪系统里，负责把影像的取样位置，生成一束光线。
由于影像的大小是可变的(多少像素宽x多少像素高)，为方便计算，这里设定一个统一的取样座标(sx, sy)，以左下角为(0,0)，右上角为(1 ,1)。
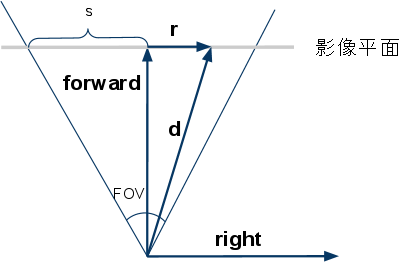
从数学角度来说，摄影机透过投影(projection)，把三维空间投射到二维空间上。常见的投影有正投影(orthographic projection)、透视投影(perspective projection)等等。这里首先实现透视投影。
透视摄影机比较像肉眼和真实摄影机的原理，能表现远小近大的观察方式。透视投影从视点(view point/eye position)，向某个方向观察场景，观察的角度范围称为视野(field of view, FOV)。除了定义观察的向前(forward)是那个方向，还需要定义在影像平面中，何谓上下和左右。为简单起见，暂时不考虑宽高不同的影像，FOV同时代表水平和垂直方向的视野角度。

上图显示，从摄影机上方显示的几个参数。 forward和right分别是向前和向右的单位向量。
因为视点是固定的，光线的起点不变。要生成光线，只须用取样座标(sx, sy)计算其方向d。留意FOV和s的关系为：tan(fov/2).
把sx从[0, 1]映射到[-1,1]，就可以用right向量和s，来计算r向量。
代码实现：
perspectiveCamera.h


接下来我们来渲染一下交点法向量，法向量是一个单位向量，在计算交点的时候们就将其存储在result.normal中了，其每个元素的范围是[-1, 1]。把单位向量映射到颜色的常用方法为，把(x, y, z)映射至(r, g, b)，范围从[-1, 1]映射至[0, 255]。
代码实现：

球体上方的法向量是接近(0, 1, 0)，所以是浅绿色(0.5, 1, 0.5)。
结语入门篇就先到这里，通过一步步搭建我们的场景，对光线追踪有了一个基础的理解,接下来我们会一步步深入一些高级的主题，比如材质，光照，雾...
参考：用JavaScript玩转计算机图形学(一)光线追踪入门-http://www.cnblogs.com/miloyip/archive/2010/03/29/1698953.html
光线追踪技术的理论和实践(面向对象)-http://blog.csdn.net/zhangci226/article/details/5664313Wikipedia, Ray Tracing
计算机图形学（第三版）（美）赫恩 著，（美）巴克 著。