快速排序法（三）
明
之前的是快速排序法的效率之一，在的快速排序法的方式更加快了快速排序法的效率，它是自演算法名 Introduction to Algorithms 之中。
解法
先明快速排序法的概念，它以最右（或最左）的值s作比的，整列分三部份，一是小於s的部份，一是大於s的部份，一是未理的部份，如下所示 ：


在排序的程中，i j 都不的往右行比交，最後列以下的：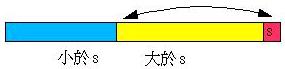


然後s的值置於中，接下就以相同的步左右的列行排序的作，如下所示：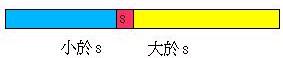


整演算的程，直接摘中的作明：

QUICKSORT(A, p, r)     if p < r         then q <- PARTITION(A, p, r)                  QUICKSORT(A, p, q-1)                  QUICKSORT(A, q+1, r) end QUICKSORT PARTITION(A, p, r)     x <- A[r]     i <- p-1     for j <- p to r-1         do if A[j] <= x                  then  i <- i+1                          exchange A[i]<->A[j]     exchange A[i+1]<->A[r]     return i+1 end PARTITION  

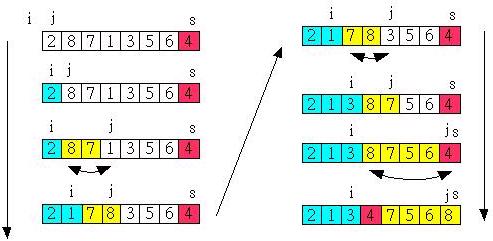
public class Sort {    public static void quick(int[] number) {        sort(number, 0, number.length-1);    }        private static void sort(int[] number, int left, int right) {        if(left < right) {             int q = partition(number, left, right);             sort(number, left, q-1);             sort(number, q+1, right);         }     }    private static int partition(int number[], int left, int right) {          int i = left - 1;         for(int j = left; j < right; j++) {             if(number[j] <= number[right]) {                 i++;                 swap(number, i, j);             }         }         swap(number, i+1, right);         return i+1;     }     private static void swap(int[] number, int i, int j) {        int t = number[i];         number[i] = number[j];         number[j] = t;    }}