数据结构查找(2)--平衡的二叉查找树(AVL树)
上篇博客介绍了二叉查找树，来看下各项操作的时间复杂度。

查找 插入 删除o(log n ) o(1) o(1)有序 链表 链表

我们可以想象下，在构造二叉查找树的时候，如果按以下递增序列构造如：2 4 5 6 7 8，那么构造出来的查找二叉树将会是接近链表的形式，这样就增加了查找的时间复杂度。
也就是说，这课树失去了平衡。我们看看下面这个图就明白了。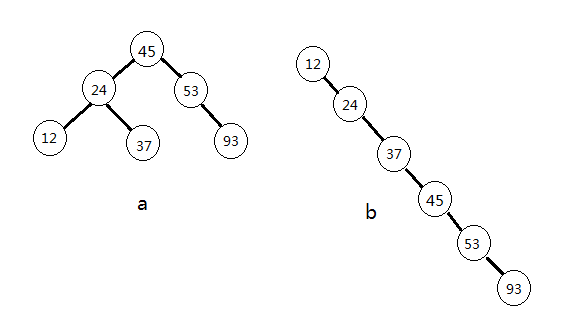

这样一来，b虽然也是一颗二叉查找树，但是查找效率大大下降。所以，我们引入了平衡的二叉查找树（AVL）树。

1.平衡
关键是“平衡”这个概念的理解。
定义如下:
树中每个结点的左、右子树深度之差的绝对值不大于1

节点的平衡因子是它的左子树的高度减去它的右子树的高度（有时相反）。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。
下面给个例子，我们以左子树的高度减去它的右子树的高度作为平衡因子。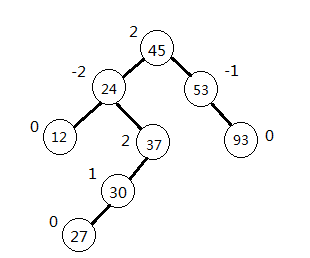


2.旋转
平衡树的关键，就是如何达到平衡，这里的关键技术就是旋转了。

下面引出的是基本概念：

有四种种情况可能导致二叉查找树不平衡，分别为：

（1）LL：插入一个新节点到根节点的左子树（Left）的左子树（Left），导致根节点的平衡因子由1变为2

（2）RR：插入一个新节点到根节点的右子树（Right）的右子树（Right），导致根节点的平衡因子由-1变为-2

（3）LR：插入一个新节点到根节点的左子树（Left）的右子树（Right），导致根节点的平衡因子由1变为2

（4）RL：插入一个新节点到根节点的右子树（Right）的左子树（Left），导致根节点的平衡因子由-1变为-2

针对四种种情况可能导致的不平衡，可以通过旋转使之变平衡。有两种基本的旋转：

（1）左旋转：将根节点旋转到（根节点的）右孩子的左孩子位置

（2）右旋转：将根节点旋转到（根节点的）左孩子的右孩子位置
给大家看张wiki上面的图，一目了然：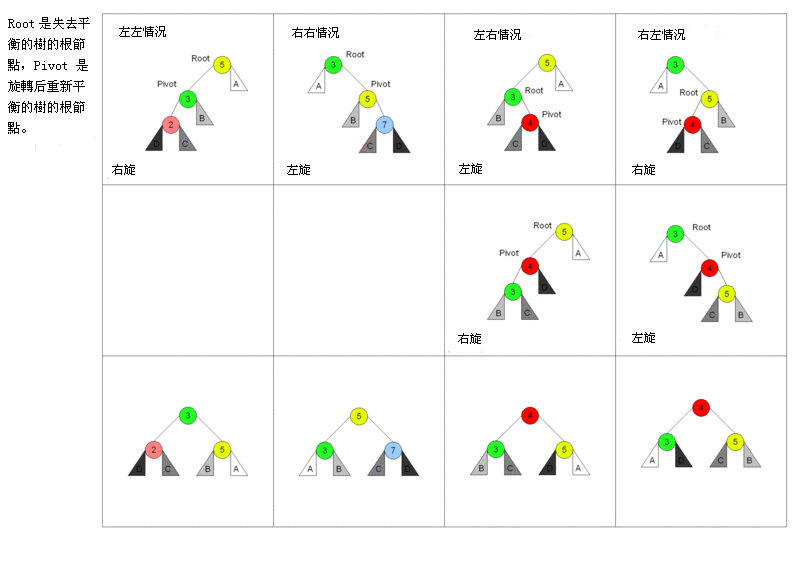



2.1 左左(LL)情况
针对左左这种情况，我们需要右旋。看上面的图就应该很明白。
我看人家的代码，这种情况的函数名叫做RightRotate，后来自己写着写着因为函数名把自己给搞晕了。所以我的函数是这样命名的：
左左情况，函数名就叫LeftLeft，这样就不用引入什么左旋右旋这样的概念了。免得把自己搞乱。如果大家不喜欢的话可以按照自己的理解来~~
我们附上代码：

AVLTree.cpp
#include "AVLTree.h"//functionsvoid Chose();void Insert();void Output(AVLTree T);void PrintTree(AVLTree T);void Delete();int main(){while (1){Chose();switch(chos){case 'i':Insert();break;case 'd':Delete();break;case 'e':exit(0);}}return 0;}void Chose(){printf("i) Insert a point \n"   "d) Delete a point \n"   "e) exit  \n"   "Input your choise \n");scanf("%c", &chos);getchar();}void Insert(){printf("\nInput the point you want to Insert: ");scanf("%d", &input);getchar();T = AVLInsert(T);Output(T);}void Output(AVLTree T){if (T == NULL)printf("None\n");else{printf("%d\troot\n", T->data);PrintTree(T);}}//Tree printvoid PrintTree(AVLTree T){if (T->lchild){printf("Lchild\t%d\t[parent:%d]\n", T->lchild->data, T->data);PrintTree(T->lchild);}if (T->rchild){printf("Rchild\t%d\t[parent:%d]\n", T->rchild->data, T->data);PrintTree(T->rchild);}}void Delete(){}



文献参考：

图片参考：
http://zh.wikipedia.org/wiki/AVL%E6%A0%91
基本概念参考：
http://dongxicheng.org/structure/avl/
代码参考：
http://www.asiteof.me/2010/06/avl/