图的底层实现
1.图数据结构出现的背景
上面几篇内容都是关于树,树在表示层次关系的数据类型时很适合,但是也仅限于“parent-child”的表示,兄弟节点等其他关系只能间接的表示,而图“graph”就能很好的弥补这个缺陷。
图的应用也很广泛,我也遇到过,例如网络中的路由器在路径的选择上就是根据最小路径的算法;在进行用户行为分析时,也可以将用户的行为轨迹对应成图,进而对图进行分析,例如有哪些功能并没有使用,在哪个位置遇到了问题等等。
该篇文章主要介绍图的底层实现。
2.图的表示图的表示方式有很多,有两种比较典型数据结构:邻接表和矩阵。
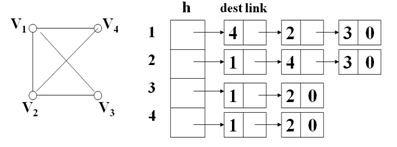
2.1邻接表对于每个顶点,如果有与其他节点连接,则依次用链表的形式将其他顶点放在该顶点后,如下图所示
2.2邻接矩阵
矩阵的大小等于顶点数*顶点数,如有顶点a,b连接,则用1表示;否则为0
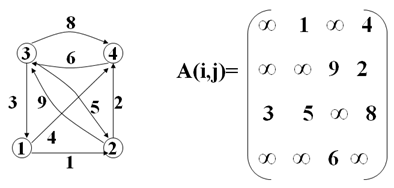
其代码表示如下,主要需要一个矩阵记录顶点是否连接。
//最小路径Dijkstra算法,一般是在有向图中 public voidDijkstra(int first){ //把所有节点的值都设置成无限大 for(int i=0; i<maxVertices;i++){ currentDist[i] =10000000;//每个节点的currentDist的值设置成无限大 } currentDist[first]= 0; for(int i =0; i<maxVertices; i++){ toBeChecked.add(newInteger(i)); } while(!toBeChecked.isEmpty()){ intminPosition = minDist(); toBeChecked.remove(minPosition);//把最小权值的节点移出toBeChecked for(int i =0; i<toBeChecked.size();i++){ intposition = toBeChecked.get(i);//获得节点 intdistance = matrix[minPosition][position];//获得的节点与最小节点间的距离 //满足条件则说明distance不是无限大,即有连接 if(currentDist[position]>currentDist[minPosition]+distance){ currentDist[position]=currentDist[minPosition]+distance; } } } } //找出toBeChecked中拥有当前权值最小的点 public intminDist(){ intminPosition = 0; for(int i=1; i<toBeChecked.size();i++){ if(currentDist[i]<minPosition) minPosition = i; } returnminPosition; }缺点:Dijkstra算法不适合负数的情况,可能导致某条边没考虑进去
4.2FordAlgorithm为了弥补Dijkstra算法的缺点,提出了FordAlgorithm,在Dijkstra的基础上进行优化的:直到处理完了整个图才最终决定每个点的最短路径。为了方便起见,写出了该算法的伪码。
FordAlgorithm(diagraph, vertex first)
forall vertices v
currentDist(V) = 无穷大;
currentDist(first)= 0;
whilethere is an edge(VU) such that currentDist(U) >currentDist(V)+weight(edge(VU))
currentDist(U)= currentDist(V)+weight(edge(VU))
缺点:在每次循环中要检查每一条边,这不是很有必要,于是有了下面的改进算法。
4.3LabelCorrectingAlgorithm该算法中不需要每次都检查每条边,而是距离发生了改变才检查。
labelCorrectingAlgorithm(diagraph,vertex first)
forall vertices v
currentDist(V)= 无穷大;
currentDist(first)= 0;
toBeChecked= {first};
while(toBeCheckedis not empty)
v= a vertex in toBeChecked;
removev from toBeChecked;
forall vertices u adjacent to V
ifcurrentDist(u) > currentDist(v) +dist(uv)
currentDist(u)= currentDist(v) + dist(uv)
add u to toBeChecked;
看最后一句,只有某个节点的距离发生了改变后,才会重新检查该节点的邻接节点。
那么怎么管理toBeChecked呢?一种方法是用队列,将距离发生改变的节点一次放入队列中,但是会造成问题:可能会有节点重复出现在队列中(例如c->d,c->g,g->d)。解决方案:将第一次放入toBeChecke中的节点放在末尾,避免第一次放入的节点重复计算。
5.Cycle环检测使用深度优先遍历算法来检测环的回路。
5.1非有向图cycleDetectionDFS(v)
num(v)= i++;//i的初始值为1
forall vertices u adjacent to v;
ifnum(u) = 0
attachedge(uv) to Edge;
cycleDetectionDFS(u);
elseif edge(uv) not in Edge//即U已经遍历过了,但不是通过uv
cycledetected;
5.2有向图
diagraphCycleDetectionDFS(v)
num(v)= i++;//i的初始值为1
forall vertices u adjacent to v;
ifnum(u) = 0
pred(u) = v;
diagraphCycleDetectionDFS(u);
elseif num(u) is not 无穷大
pred(u)= v;
cycledetected;
num(v)= 无穷大//通过该句,程序只会在最深层(检测到环路)才会执行else if语句