Graph(2)-Graphs Traverse

1 Preface

There are many algorithm about graph, but traverse algorithm is the most important algorithm. For example, crawl all the webpage from the Internet need used the traverse algorithm. There are two common algorithms to traverse a graph: depth-first- search(DFS,深度优先算法) and breadth-first search(BFS,广度优先算法).The depth-first search is implemented with a stack(the content of the stack is the route you took from the starting vertex to get where you are), whereas the breadth-first search is implemented with a queue.

2 Depth-First Search

2.1 Step

The depth-first search likes to get far away from the starting point as quickly as possible and returns only when it reaches a dead end(一条路走到黑), so the term depth means the distance from the starting point. The depth-first search steps are:

1) push in stack(rule 1): If possible, visit an adjacent unvisited vertex, mark it, and push it in the stack.

2) pop off stack(rule 2): If you can't follow rule1, then, if possible, pop a vertex off the stack.

3)stack is empty(rule 3): If you can't follow rule1 or rule2, you're done.

2.2 Example

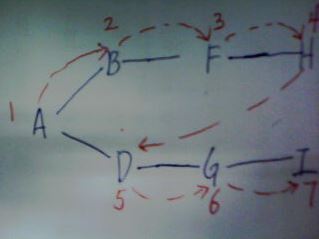
Now I use the following graph describes these steps.

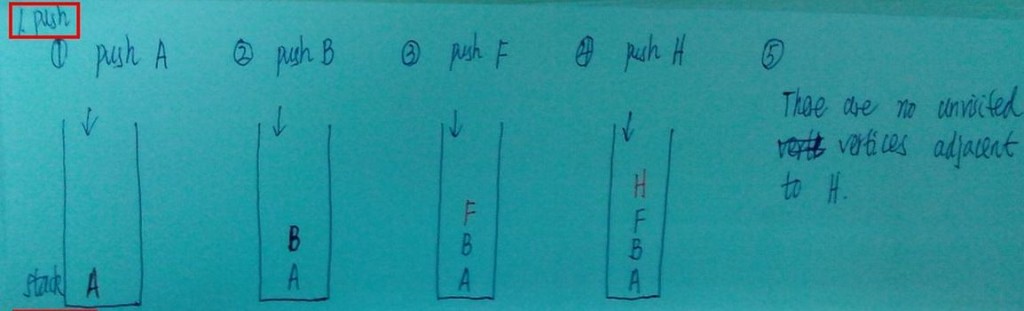
1)push in stack

To carry out the depth-first search, you pick a starting point-in this case, vertex A.

Next, push any vertex adjacent to A that hasn't yet been visited.We'll assume the vertices are selected in alphabetical order, so that bring up B. You visit B, mark it(visited), and push it on the stack.

Now you're at B, do the same thing as before: go to adjacent vertex that hasn't been visited.Then F、H pushed in stack. The push steps are like the following figure:

2) pop off stack

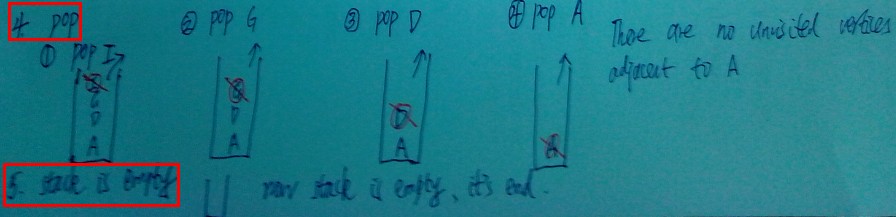
Now you're at H, there are no adjacent vertices adjacent to H.Then following rule 2, you pop H off the stack, which bring you back to F. Now do the same thing as before: rule1, then rule2: the vertex has no unvisited adjacent vertices, pop it. So F、B are popped off the stack.

3) push in stack and pop off stack

Now you're at A, there are adjacent vertices to A. Then do the same thing following rule1 and rule2. So D、G、I are pushed in stack, then I、G、D are popped off the stack. Now you are at A, has no unvisited vertices, so pop A off the stack.

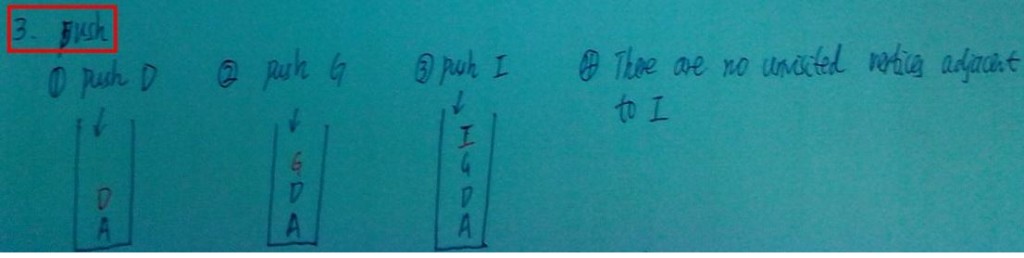
4) stack is empty

Now there is nothing left in stack, which brings up rule3: stack is empty.

We can get the order in which you visit the vertices from the content of the stack:ABFHDGI

2.3 Java Implement

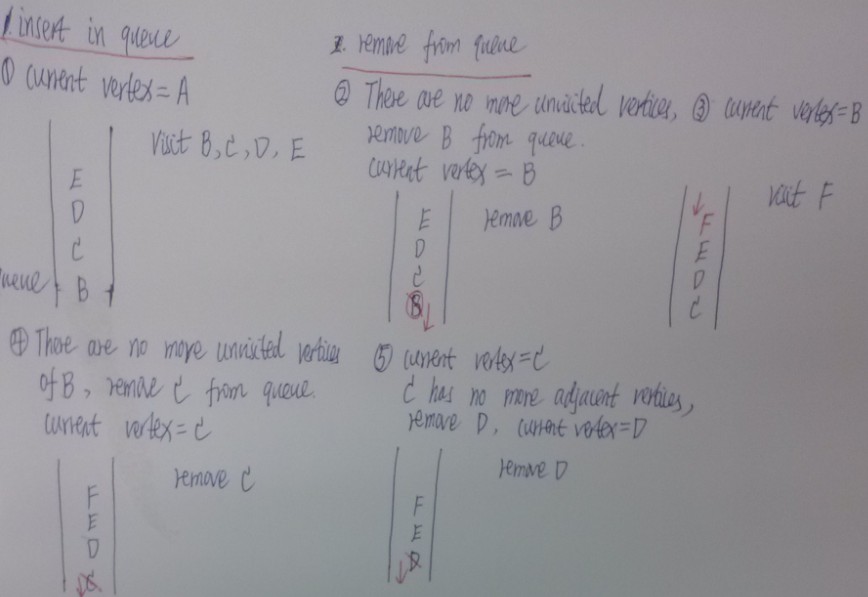
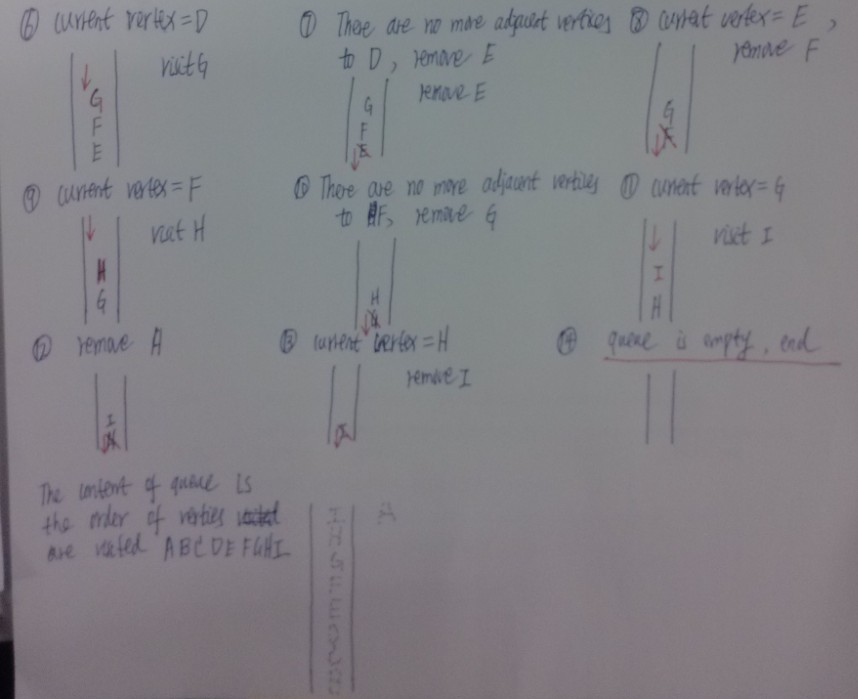
A is the current vertex, s you visit  it and make it the current vertex. Then visit A's adjacent vertices, mark it ,and insert it into the queue, so insert B,C,D,E are inserted in the queue.
Now A has no more unvisited vertices, then remove vertex B from  queue. So now B is the current vertex. Do these steps until queue is empty,then end .


The content of the queue is the route you took from the starting point to the current vertex. The nodes are visited in the order ABCDEFGHI.
3.3 Java Implement
// bfs.java// demonstrates breadth-first search// to run this program: C>java BFSApp////////////////////////////////////////////////////////////////class Queue   {   private final int SIZE = 20;   private int[] queArray;   private int front;   private int rear;// -------------------------   public Queue()            // constructor      {      queArray = new int[SIZE];      front = 0;      rear = -1;      }// -------------------------   public void insert(int j) // put item at rear of queue      {      if(rear == SIZE-1)         rear = -1;      queArray[++rear] = j;      }// -------------------------   public int remove()       // take item from front of queue      {      int temp = queArray[front++];      if(front == SIZE)         front = 0;      return temp;      }// -------------------------   public boolean isEmpty()  // true if queue is empty      {      return ( rear+1==front || (front+SIZE-1==rear) );      }// -------------------------   }  // end class Queue////////////////////////////////////////////////////////////////class Vertex   {   public char label;        // label (e.g. 'A')   public boolean wasVisited;// -------------------------   public Vertex(char lab)   // constructor      {      label = lab;      wasVisited = false;      }// -------------------------   }  // end class Vertex////////////////////////////////////////////////////////////////class Graph   {   private final int MAX_VERTS = 20;   private Vertex vertexList[]; // list of vertices   private int adjMat[][];      // adjacency matrix   private int nVerts;          // current number of vertices   private Queue theQueue;// ------------------------   public Graph()               // constructor      {      vertexList = new Vertex[MAX_VERTS];                                          // adjacency matrix      adjMat = new int[MAX_VERTS][MAX_VERTS];      nVerts = 0;      for(int j=0; j<MAX_VERTS; j++)      // set adjacency         for(int k=0; k<MAX_VERTS; k++)   //    matrix to 0            adjMat[j][k] = 0;      theQueue = new Queue();      }  // end constructor// -------------------------   public void addVertex(char lab)      {      vertexList[nVerts++] = new Vertex(lab);      }// -------------------------   public void addEdge(int start, int end)      {      adjMat[start][end] = 1;      adjMat[end][start] = 1;      }// -------------------------   public void displayVertex(int v)      {      System.out.print(vertexList[v].label);      }// -------------------------   public void bfs()                   // breadth-first search      {                                // begin at vertex 0      vertexList[0].wasVisited = true; // mark it      displayVertex(0);                // display it      theQueue.insert(0);              // insert at tail      int v2;      while( !theQueue.isEmpty() )     // until queue empty,         {         int v1 = theQueue.remove();   // remove vertex at head         // until it has no unvisited neighbors         while( (v2=getAdjUnvisitedVertex(v1)) != -1 )            {                                  // get one,            vertexList[v2].wasVisited = true;  // mark it            displayVertex(v2);                 // display it            theQueue.insert(v2);               // insert it            }   // end while         }  // end while(queue not empty)      // queue is empty, so we're done      for(int j=0; j<nVerts; j++)             // reset flags         vertexList[j].wasVisited = false;      }  // end bfs()// -------------------------   // returns an unvisited vertex adj to v   public int getAdjUnvisitedVertex(int v)      {      for(int j=0; j<nVerts; j++)         if(adjMat[v][j]==1 && vertexList[j].wasVisited==false)            return j;      return -1;      }  // end getAdjUnvisitedVertex()// -------------------------   }  // end class Graph////////////////////////////////////////////////////////////////class BFSApp   {   public static void main(String[] args)      {      Graph theGraph = new Graph();      theGraph.addVertex('A');    // 0  (start for bfs)      theGraph.addVertex('B');    // 1      theGraph.addVertex('C');    // 2      theGraph.addVertex('D');    // 3      theGraph.addVertex('E');    // 4      theGraph.addEdge(0, 1);     // AB      theGraph.addEdge(1, 2);     // BC      theGraph.addEdge(0, 3);     // AD      theGraph.addEdge(3, 4);     // DE      System.out.print("Visits: ");      theGraph.bfs();             // breadth-first search      System.out.println();      }  // end main()   }  // end class BFSApp////////////////////////////////////////////////////////////////