货郎问题 Java 实现
我使用的方法是:
假设图有n个顶点, 若干条边
1) 从所有边中找到 n-1 条边构成选择组合
2) 从权值和最小的组合开始验证边能否这个组合能遍历所有的顶点
如果能遍历则找到答案
因此算法的关键是:
1) 找子集合并按权值和排序, 这个问题我在这篇文章中提到
http://blog.csdn.net/span76/article/details/8755416
我的验证方法是, 统计边集合的顶点, 每个顶点的统计值不能为 0, 也不能大于2
程序我放在最后, 其操作方式是:
1) 鼠标左键选下一个组合(不验证)
2) 鼠标右键验证当前组合,如果不满足, 自动找到下一个能构成路径的组合
运行的结果
满足条件的组合
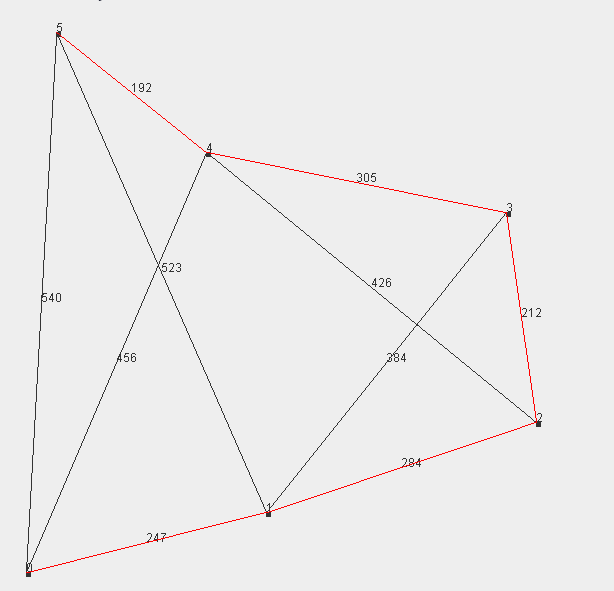
不满足条件的组合

下一个满足条件的组合
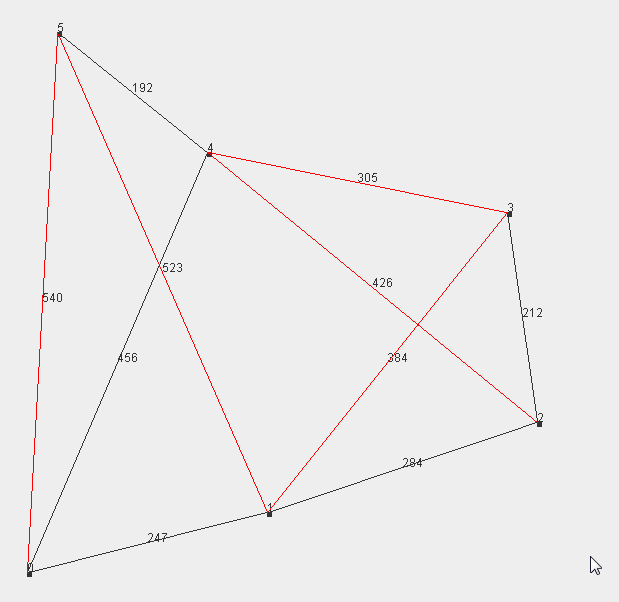
public class Main extends Component implements MouseListener { public static void main(String[] args) { WindowListener l = new WindowAdapter() { public void windowClosing(WindowEvent e) { System.exit(0); } }; JFrame f = new JFrame("A JFrame"); f.setSize(800, 800); f.addWindowListener(l); Main m = new Main(); f.add(m); f.addMouseListener(m); f.setVisible(true); } public Dimension getPreferredSize() { return new Dimension(800, 800); } //--------------- mouse event ----------- @Override public void mouseClicked(MouseEvent e) { if (e.getButton() == MouseEvent.BUTTON1) { //System.out.print("left"); this.selectNext(); this.repaint(); }else if (e.getButton() == MouseEvent.BUTTON3) { //System.out.print("right"); while (!this.pathIsOK() ) { this.selectNext(); } this.repaint(); } } @Override public void mouseEntered(MouseEvent arg0) {} @Override public void mouseExited(MouseEvent arg0) {} @Override public void mousePressed(MouseEvent arg0) {} @Override public void mouseReleased(MouseEvent arg0) {} ///--------------- mouse event ----------- public void paint(Graphics g) { Graphics2D g2d = (Graphics2D) g; for (int i = 0; i < mPoints.length; i++) { g2d.fillRect(mPoints[i].x, mPoints[i].y, 5, 5); } for (int i = 0; i < mReachs.length; i++) { for (int j = 0; j < mReachs[i].length; j++) { if (mReachs[i][j] > 0) { int x1 = mPoints[i].x; int y1 = mPoints[i].y; int x2 = mPoints[j].x; int y2 = mPoints[j].y; g2d.drawLine(x1, y1, x2, y2); g2d.drawString(String.valueOf(i), x1, y1); int mid_x = (x1 + x2) / 2; int mid_y = (y1 + y2) / 2; g2d.drawString(String.valueOf(mReachs[i][j]), mid_x, mid_y); } } } drawSelected(g); } class Point { public int x; public int y; public Point(int x, int y) { this.x = x; this.y = y; } } class Edge implements Comparable<Edge> { public int Point1; public int Point2; public int weight; public Edge(int Point1, int Point2, int weight) { this.Point1 = Point1; this.Point2 = Point2; this.weight = weight; } @Override public int compareTo(Edge o) { if ( this.weight < o.weight) return -1; else if( this.weight > o.weight) return 1; return 0; } } // define point Point mPoints[] = { new Point(10, 100), new Point(50, 90), new Point(95, 75), new Point(90, 40), new Point(40, 30), new Point(15, 10) }; // 0: self 1:reachable -1:unreadable int mReachs[][] = { { 0, 1, -1, -1, 1, 1 }, { 1, 0, 1, 1, -1, 1 }, { -1, 1, 0, 1, 1, -1 }, { -1, 1, 1, 0, 1, -1 }, { 1, -1, 1, 1, 0, 1 }, { 1, 1, -1, -1, 1, 0 } }; ArrayList<Edge> mRemainEdges = new ArrayList<Edge>(); ArrayList<Edge> mSelectEdges = new ArrayList<Edge>(); int SELECT_COUNT = 0; private void init() { // make position large for (int i = 0; i < mPoints.length; i++) { mPoints[i].x *= 6; mPoints[i].y *= 6; } //calculate distance for (int i = 0; i < mReachs.length; i++) for (int j = i; j < mReachs[i].length; j++) { if (mReachs[i][j] > 0) { int x1 = mPoints[i].x; int y1 = mPoints[i].y; int x2 = mPoints[j].x; int y2 = mPoints[j].y; int distance = (int) Math.sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)); mReachs[i][j] = distance; mRemainEdges.add( new Edge(i,j,distance)); // constructor edge mReachs[j][i] = distance; } } Collections.sort(mRemainEdges); SELECT_COUNT = mReachs.length -1; // for n points, we will should select n+1 edge for (int i=0; i<SELECT_COUNT; i++) mSelectEdges.add( mRemainEdges.remove(0)); print(mSelectEdges); // print initial mSelectEdges } boolean selectNext() { while( mRemainEdges.size() > 0) { Edge cur = mRemainEdges.get(0); int pos = Collections.binarySearch(mSelectEdges, cur); if (pos < 0) // binarySearch (-(insertion point) - 1) pos = (-pos) -1; else { System.err.print("Not allow equal elements"); System.exit(-1); // Not allow equal elements } if ( pos == 0 ) {// that means current element is less that any in selects, we won't need to consider this elem mRemainEdges.remove(0); continue; } else { int insert_pos = pos-1; mRemainEdges.set(0,mSelectEdges.get(insert_pos)); mSelectEdges.set(insert_pos, cur); print(mSelectEdges); return true; } } System.out.println(" no next to select"); return false; } boolean pathIsOK() { int[] points = new int[ mPoints.length]; for (int i=0; i <mSelectEdges.size(); i++ ) { Edge e= mSelectEdges.get(i); points[e.Point1] ++; points[e.Point2] ++; } for (int i=0; i<points.length; i++) { if ( points[i] ==0 || points[i] > 2 ) return false; } System.out.print(" --OK--"); print(mSelectEdges); return true; } /* void findPaths() { while (selectNext()) { if ( pathIsOK() ) break; } } */ static void print(ArrayList<Edge> mSelectEdges2 ) { int sum = 0; for (int i=0; i< mSelectEdges2.size(); i++) { sum += mSelectEdges2.get(i).weight; System.out.print( " " + mSelectEdges2.get(i).weight); } System.out.println(" sum:"+sum ); } public Main() { init(); //findPaths(); } void drawSelected( Graphics g) { Graphics2D g2d=(Graphics2D)g; g2d.setColor(Color.RED); for (int i=0; i< mSelectEdges.size(); i++) { Edge e= mSelectEdges.get(i); int x1 = mPoints[e.Point1].x; int y1 = mPoints[e.Point1].y; int x2 = mPoints[e.Point2].x; int y2 = mPoints[e.Point2].y; g2d.drawLine(x1,y1,x2,y2); } }}