利用简单的一元线性回归分析估计软件项目开发时间

????? 至于这个公式为什么能反映出两个变量的相关性，可以去参考高等数理统计相关资料，本文不再赘述，只是顺便说一下，r的范围在-1~1之间，绝对值越大代表相关性越强，如果为正值则表示两个变量正相关，否则为负相关。知道了这个，我们这一步骤的目的就是找出候选Proxy中与y相关系数最大的作为x。

????? 不过，这数据从哪里来呢？这就要从以前做过的项目中提取了。查阅朋友所在团队最近做过的5个项目的数据资料（这里当然历史项目越多越好，不过笔者这个朋友的团队只有5个项目的记录），得到如下数据：

????? 项目工期（y）：???? 424???? 267???? 90???? 331???? 160???? （人时）

????? 用例数量（x1）：?? 37?????? 20?????? 6?????? 18?????? 12

????? 实体数量（x2）：???15?????? 9???????? 4???????11?????? 14

????? 数据表数量（x3）：?25??????18?????? 7???????16?? ????18

????? 下面就是计算各个相关系数了，计算相关系数是一项机械且乏味的活动，一般都会交由相应的工具去完成。不过您要是感兴趣，也可以自己代入上述公式手算。下图是我用Excel计算的结果：

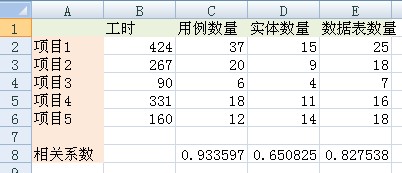??????图1

????? 一般来说，|r|大于0.7就有很好的相关性了，而从计算结果可以看出，用例数量x1和工期y的相关系数达到0.93，最为优秀，而数据表数量x3也达到0.83，唯有实体数量x2的相关系数仅为0.65，质量较差。因为|r(x2,y)|<0.7，所以这里首先排除掉。

????? 到了这里似乎我们可以顺利成章选择x1作为最终Proxy，但是还有一点要考虑，就是显著性。所谓显著性就是在偶然情况下得到此结果的概率，如果显著性不足，说明这个结果不可靠。显著性t值的计算公式如下：

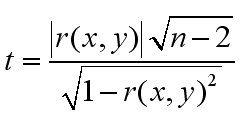
????? 因为n=5，这里自由度为3，然后查询t分布表，得到95%预测区间为3.182。因为一般显著性<0.05则认为显著性较好，所以如果t的值大于3.182，我们则可以接受。不过如果使用工具的话，一般可以用t检测直接得出显著性，这里我用Excel得到r(x1,y)的显著性为0.006，r(x3,y)的显著性为0.007（如图2所示），都远小于0.05，显著性均非常好。所以根据择优录取原则，我们选择x1：需求文档中用例数量作为预测Proxy。

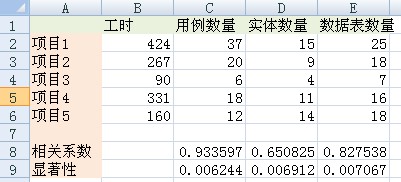
图2

得到x的值

????? 在上文中，我们通过相关性和显著性分析，最终决定使用需求文档中的用例数量作为x。下面就是要确定x的值，这个不必多说，直接从需求文档中得到相应的数量即可。

确定相关函数f

????? 知道了x的值，下面就是要确定相关函数了。这一步是最艰难也是最有技术性的，因为相关函数不但和数理因素相关，还与开发团队、团队中的人以及管理方法有关。如果人员变动很大或管理方法做了很大的调整，历史数据可能就不具备参考价值了。不过如果团队的开发水平和管理方法没有重大变动，这个函数还是相对稳定的。

????? 在函数选型上，一般会选择线性函数，当然我个人对此是十分怀疑的，但是这里为了简单起见，我们姑且照例使用线性函数作为预测模型。这样可以建立一元线性回归模型如下：

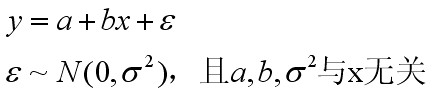
????? 这个函数并不是简单的线性函数，而是包含了一个随机变量ε，这是一个服从正态分布的随机变量。上述模型的直观意义可以如下描述：a代表与x即用例数量无关的起始时间，b代表每一个用例所耗费的平均时间，而ε代表开发中的不确定性。在不同的团队中或不同的管理方法下，a,b和ε都是不一样的，但是当团队和管理方法相对稳定，可以认为a,b和ε是可通过历史数据估计的。而因为ε的期望为0，所以只要给出a和b的合理估计，就可以得到y的一个无偏估计。

????? 下面我们估计a和b的值。估计方法有很多，如曲线拟合法或最小二乘法。这里我们采用最小二乘法进行估计。

????? 最小二乘法估计的基本原理如下：

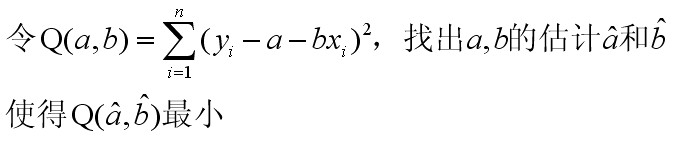
????? 求极值可以使用微积分中的求极值方法，首先令Q(a,b)对a和b分别求偏导，并令偏导为零，得如下方程组：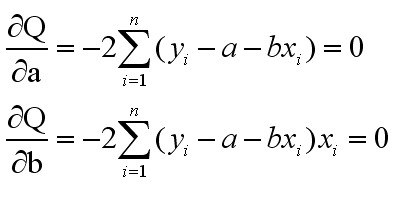

????? 经过一系列计算和推导，最终可得到:

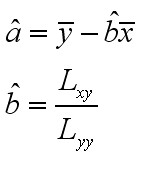
????? 将以前的历史数据代入上述方程，就可以得到a和b的最小二乘估计。同样，这种机械而乏味的计算一般交由工具去完成。我用Excel得到a和b的估计分别为56.251和10.653。Excel分析结果如图3所示：

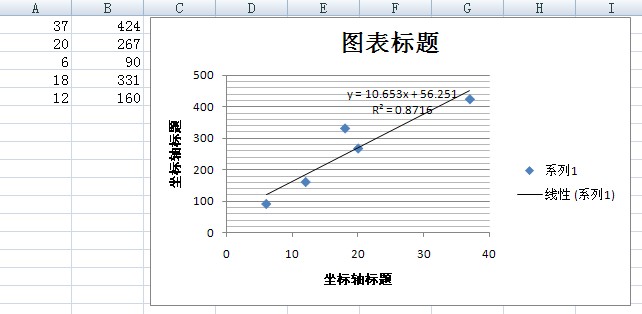
图3

????? 根据估计结果，我们可以得出相关函数为y=56.251+10.653。我们还可以证明，这个估计是一致最小方差无偏估计，证明过程从略。

????? 现在我们不但得到了相关函数，还得到了如下有用的数据结果：这个团队在目前的管理模式下，开发一个项目平均准备时间为56.251人时，而平均每个用例开发耗时为10.653人时。

得出y

????? 有了上面的结果，我们可以很轻易得出新项目的计划工时。例如新项目有50个用例，代入可以得到y=56.251+10.653*50=588.901，约为589个人时，再假设团队中有3个开发人员，平均每周工作五天，每天工作8小时，就可以得到项目大约需要开发24.54个人日，开发周期约为5周。

后面的话

????? 至此我们已经完成了利用一元线性回归模型对软件工期的估计。但是不得不承认，这个估计方法存在很多缺陷，如估计变量单一以及估计模型过于简单等等。实验证明，这种一元线性模型对中小型项目相对有效，如果团队比较大并且项目十分复杂，估计效果就不理想了。不过这篇文章给出了一种思路，就是如何利用数理统计模型以及历史经验数据来估计新项目的工期。对于文中的具体方法则可以进行诸多扩展，例如使用多个估计代理进行多元回归分析、细化估计方法等等。例如PSP中就给出一种非常精细的PROBE估计法，有兴趣的朋友可以参考。另外，除了求得估计值，还可以给出估值置信区间，甚至使用蒙特卡洛模拟技术进行更复杂的分析，都可以得到更理想的估值。但是其核心思想与本文是相通的。