数学之路(3)-机器学习(3)-机器学习算法-余弦相似度(1)
余弦相似性是指通过测量两个向量内积空间的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1,而其他任何角度的余弦值都不大于1;并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时,余弦相似度的值为1;两个向量夹角为90°时,余弦相似度的值为0;两个向量指向完全相反的方向时,余弦相似度的值为-1。在比较过程中,向量的规模大小不予考虑,仅仅考虑到向量的指向方向。余弦相似度通常用于两个向量的夹角小于90°之内,因此余弦相似度的值为0到1之间。
值得注意的是余弦相似度可以用在任何维度的向量比较中,它尤其在高维正空间中的利用尤为频繁。
两个向量间的余弦值可以很容易地通过使用欧几里得点积和量级公式推导:
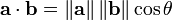
鉴于两个向量的属性, A 和B的余弦相似性θ用一个点积形式来表示其大小,如下所示:
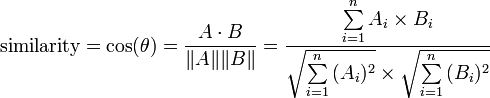
产生的相似性范围从-1到1:-1意味着两个向量指向的方向正好截然相反,1表示它们的指向是完全相同的,0通常表示它们之间是独立的,而在这之间的值则表示中度的相似性或相异性。
余弦相似度很适合做文本分类,我们把文本中的所有词映射到n维空间的一个向量
我们先下载和测试中文分词组件:"结巴"中文分词,该组件通过import jieba 来引用,如:
#!/usr/bin/env python#-*- coding: utf-8 -*-#code:myhaspl@qq.comimport cv2import numpy as npimport jiebadef get_cossimi(x,y): myx=np.array(x) myy=np.array(y) cos1=np.sum(myx*myy) cos21=np.sqrt(sum(myx*myx)) cos22=np.sqrt(sum(myy*myy)) return cos1/float(cos21*cos22) if __name__ == '__main__': print 'http://blog.csdn.net/myhaspl' print 'myhaspl@qq.com' print print 'loading %s ...' % fn print 'working', f1 = open('mobile1.txt') try: f1_text = f1.read( ) finally: f1.close( ) f1_seg_list = jieba.cut(f1_text) print "Full Mode:", "/ ".join(f1_seg_list)