从排序开始（四）快速排序

快速排序是由东尼霍尔所发展的一种使用分治法—ivide and conquer）策略的排序算法。

它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

基本步骤为：

1、从数列中挑出一个元素，称为 "基准"

2、重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。

3、递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。

下面的图解是基于交换值的实现方法，后面我们的实现是另一种方法：

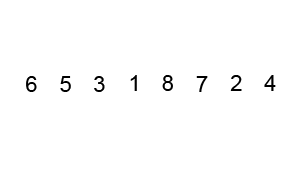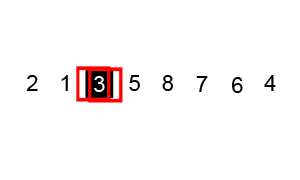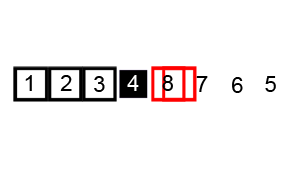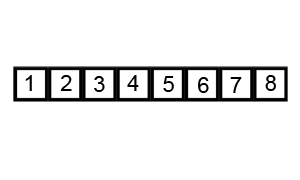
最差时间复杂度： O(n^2)

最优时间复杂度： O(n logn)

平均时间复杂度： O(n logn)

最差空间复杂度： 最好是O(log n)

稳定性：不稳定

快速排序的时间主要耗费在划分操作上，对长度为k的区间进行划分，共需k-1次关键字的比较。

最坏情况是每次划分选取的基准都是当前无序区中关键字最小(或最大)的记录，划分的结果是基准左边的子区间为空(或右边的子区间为空)，而划分所得的另一个非空的子区间中记录数目，仅仅比划分前的无序区中记录个数减少一个。时间复杂度为O(n*n)

在最好情况下，每次划分所取的基准都是当前无序区的"中值"记录，划分的结果是基准的左、右两个无序子区间的长度大致相等。总的关键字比较次数：O(nlgn)

优化：

一种比较常见的优化方法是随机化算法，即随机选取一个元素作为主元。这种情况下虽然最坏情况仍然是O(n^2），但最坏情况不再依赖于输入数据，而是由于随机函数取值不佳。实际上，随机化快速排序得到理论最坏情况的可能性仅为 1/(2^n）。所以随机化快速排序可以对于绝大多数输入数据达到O(n logn）的期望时间复杂度。

已优化实现：

void quickSort(int num[], int l, int r){    if (l >= r) return;// 在数组大小小于8的情况下使用插入排序if (r - l + 1 < 8) {for (int i = l; i <= r; i++)if (num[i] < num[i - 1])  {int j,t = num[i];for (j = i - 1; j >= 0 && num[j] > t; j--)  num[j + 1] = num[j];  num[j + 1] = t;  }return;}//随机选取基数int k = rand()%(r - l + 1) + l; int t = num[k];num[k]  = num[l];num[l] = t;    int i = l, j = r, key = num[l];    while (i < j)    {//从右向左找第一个小于等于key的数        while(i < j && num[j] > key)    j--;          if(i < j)num[i++] = num[j];// 从左向右找第一个大于等于key的数        while(i < j && num[i] < key)i++;        if(i < j)num[j--] = num[i];    }    num[i] = key;//分治，递归    quickSort(num, l, i - 1);     quickSort(num, i + 1, r);}void qSort(int num[], int n){quickSort(num,0, n-1);}