CH BR13数学(啥?-a^b≡a^b mod phi(p)+phi(p)(mod p)(b>=phi(p))公式)
啥? Beta Round #13 (数学专场)背景
有人写了一个RSA加密给我玩。
描述
我赌5毛前面两题的内容也就开头几句话平时会用到。
还是做点具体的东西吧。
求c^d Mod N
输入格式
三个用空格隔开的整数c,d,N
输出格式
一个整数表示答案
样例输入1 2 6
样例输出1
数据范围与约定对于前30%的数据: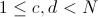 ,
,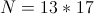 对于后70%的数据:
对于后70%的数据: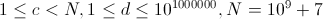
根据标题公式a^b≡a^b mod phi(p)+phi(p)(mod p)(b>=phi(p)) 变把极限搞定,
剩下的数据快速幂乱搞很容易过。。。。。
#include<cstdio>#include<cstdlib>#include<cstring>#include<iostream>#include<algorithm>#include<functional>#include<cmath>#include<cctype>#include<cassert>#include<climits>using namespace std;#define For(i,n) for(int i=1;i<=n;i++)#define Rep(i,n) for(int i=0;i<n;i++)#define Fork(i,k,n) for(int i=k;i<=n;i++)#define ForD(i,n) for(int i=n;i;i--)#define Forp(x) for(int p=pre[x];p;p=next[p])#define RepD(i,n) for(int i=n;i>=0;i--)#define MEM(a) memset(a,0,sizeof(a))#define MEMI(a) memset(a,127,sizeof(a))#define MEMi(a) memset(a,128,sizeof(a))#define INF (2139062143)#define phiF (1000000006)#define MAXN (1000000+10)typedef long long ll;ll a,b,F;char s[MAXN];ll read(){ ll p=0;int n=strlen(s+1); For(i,n) { p=(p*10+s[i]-48)%phiF; } return p+(n>10)*phiF;}ll pow2(ll a,ll b){ if (b==1) return a; if (b==0) return 1; ll p=pow2(a,b>>1); p=(p*p)%F; if (b&1) p=(p*a)%F; return p;}int main(){// freopen("ch-BR13-what.in","r",stdin);// freopen(".out","w",stdout); scanf("%lld%s%lld",&a,s+1,&F); printf("%lld\n",pow2(a,read())); // while (1); return 0;}
1
数据范围与约定对于前30%的数据: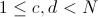 ,
,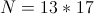 对于后70%的数据:
对于后70%的数据: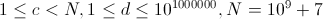
根据标题公式a^b≡a^b mod phi(p)+phi(p)(mod p)(b>=phi(p)) 变把极限搞定,
剩下的数据快速幂乱搞很容易过。。。。。
#include<cstdio>#include<cstdlib>#include<cstring>#include<iostream>#include<algorithm>#include<functional>#include<cmath>#include<cctype>#include<cassert>#include<climits>using namespace std;#define For(i,n) for(int i=1;i<=n;i++)#define Rep(i,n) for(int i=0;i<n;i++)#define Fork(i,k,n) for(int i=k;i<=n;i++)#define ForD(i,n) for(int i=n;i;i--)#define Forp(x) for(int p=pre[x];p;p=next[p])#define RepD(i,n) for(int i=n;i>=0;i--)#define MEM(a) memset(a,0,sizeof(a))#define MEMI(a) memset(a,127,sizeof(a))#define MEMi(a) memset(a,128,sizeof(a))#define INF (2139062143)#define phiF (1000000006)#define MAXN (1000000+10)typedef long long ll;ll a,b,F;char s[MAXN];ll read(){ ll p=0;int n=strlen(s+1); For(i,n) { p=(p*10+s[i]-48)%phiF; } return p+(n>10)*phiF;}ll pow2(ll a,ll b){ if (b==1) return a; if (b==0) return 1; ll p=pow2(a,b>>1); p=(p*p)%F; if (b&1) p=(p*a)%F; return p;}int main(){// freopen("ch-BR13-what.in","r",stdin);// freopen(".out","w",stdout); scanf("%lld%s%lld",&a,s+1,&F); printf("%lld\n",pow2(a,read())); // while (1); return 0;}
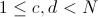 ,
,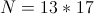 对于后70%的数据:
对于后70%的数据: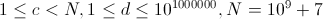
根据标题公式a^b≡a^b mod phi(p)+phi(p)(mod p)(b>=phi(p)) 变把极限搞定,
剩下的数据快速幂乱搞很容易过。。。。。