从柏拉图采花问题说起

在台大的概率课上做了一道有意思的概率题：

既然柏拉图这么聪明，不知道他这样做是不是已经知道自己能够以较大的概率摘得最美的玫瑰花了。当然，想归想，算出来才有说服力。这道题思考了一下，有下面几种思路：

思路1：

说是玫瑰花，其实模型是一个数字排列问题。
给出1-8 八个数字，问取到8的概率是多少。
我们这里给出确保能取到8的所有情况，然后除以8!即为概率。

首先我们要保证8不会出现在前三个数字里面，下面分情况讨论：

1：8出现在第四个位置，前三个数和后面的数随便排列，7!
2：8出现在第五个位置，再考虑前三个数最大的数分别是7的情况，6的情况，5的情况，4的情况
3：8出现在第六个位置，再考虑前三个数中最大的数分别是7的情况，6的情况，5的情况
4：8出现在第七个位置，再考虑前三个数中最大的数分别是7的情况，6的情况
5：8出现在最后一个位置，此时前面三个数最大的数只能是7.

思路2：

考虑前三个数字中的最大数字
如果前三个数字中的最大数字是8，那么柏拉图就没戏了
如果前三个数字中的最大数字是7，那么后面五个数字随便排
如果前三个数字中的最大数字是6，那么后面的五个数字中8一定要排在7前面
如果前三个数字中的最大数字是5，那么后面的五个数字中8一定要排在7和6前面，但7和6的顺序可变
后面就以此类推了

思路3：

1：8出现在第四个位置，剩下七中出三字在八前面，且三中的最大在前三位置之一
2：8出现在第五个位置，剩下七中出四字在八前面，且四中的最大在前三位置之一
3：8出现在第六个位置，剩下七中出五字在八前面，且五中的最大在前三位置之一
4：8出现在第七个位置，剩下七中出六字在八前面，且六中的最大在前三位置之一
5：8出现在最后一个位置，剩下七中出七字在八前面，且七中的最大在前三位置之一
以上的率和是答案。

Ps.1. 要做排列（分成前三、八以後、第四到八之，三）
Ps.2. 最大是不重要

看了这些想法相信已经明白其实就是一个数字排列问题，我们的目标是要取到8，前面3个数中出现的最大数对我们实现目标是有一定的影响的。转换过后，这道题就变得简单了，算出来保留2位小数概率为0.41。

好了，上面是个特殊的问题，现在该抛出一个一般的问题了：

我们来换一个思路，
若有n朵花，用1,2,3...n表示，数字越大越美丽
若用前m朵做参考，那取到n的概率P是多少？

假设n出现在m前，肯定没戏了，
考虑n出现在m+p+1位置，这样要求， 前m个数字的最大值，比m+1到m+p 这p个数的最大值大，就可以取到n了
所以前m个数的最大值，一定也是前m+p个数的最大值
也就是说，有m+p 个不同的数，最大值落在前m个概率的是多少？

我想，解决了这个问题，无论花园里面有几朵玫瑰花，前面看几朵作为参考我们都不害怕了。

现在说说这种思路的解法：

首先p是有范围的，因为n出现在n+1-n这个区间，p的取值为0到n-m-1

考虑前m+p个数字的情况，我们是从n-1个数中抽取出m+p个数，共C(m+p,n-1)种

再考虑其中最大的数字放在前m个位置的个数,C(1,m)

前面剩下的m+p-1个数任意排列即可，(m+p-1)!种

撇除掉n和前面m+p个数，后面的n-m-p-1任意排列，(n-m-p-1)!种

好了，加上上面p的取值，和全排列的个数 n!，我们就得到了概率的一般公式：

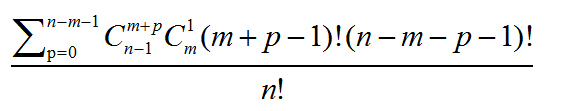
如果不信把n=8, m=3带进去试试。

好了，现在连一般的通项公式都弄出来了。

不过还没有结束，心中仍存在一个疑问，为什么柏拉图在这里知道选择先查看3朵而后采到最美玫瑰花的概率最大，一个原因是他把这里的几种情况都算了一遍，另外一种原因可以通过数学证明当m和n存在某种关系时概率最大。

为了计算，我们可以对上面的一般式进行化简，结果发现概率大小和下面这个式子的大小密切相关

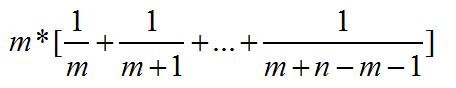
现在可以编程来看看给定n时m取什么情况式子值最大，这里n取值为2到50：

这就是传说中的调和序列求和。于是我们就可以把式子简化为：

这里要补充说明下，我们说了n很大，没有说m也很大，ln(m)放在这里有些欠妥，如果能给出证明自然是好的，无奈这里我不会证，不过我认为误差应该在我们可以接受的范围内。
有人给出证明：
令f(m)=m*[1/m+1/(m+1)+...1/(m+n-m-1)]
f(m+1)-f(m)=1/(m+1)+...+1/(n-1)-1=s(n-1)-s(m)-1
m满足s(n-1)-s(m)=1取最大，其中s(n)是调和级数的前n和，所以m也是很大的
下面对这个式子求导，令导数为0，就能得到一个很简单的结论：

其实应该写成这样较为合适：

这就是在n取值较大时m与n的关系。
如果不信，可以写程序验证下，对上面的代码改动一下即可，n值要取大一点：


可以看到，n取900多时，n/m的比值和e(2.71828182846)确实比较接近，之所以有偏差，估计一方面是在对公式化简的时候产生的，另一方面是因为m必须取整数而产生的。大体说来，结果还是令我满意的。


小结：在这里我展示了从柏拉图采花的一个特殊问题衍生到一个一般问题并求解的过程。在求解一般问题时，我先用数学知识来求出公式，然后使用了程序来验证猜想，再用数学知识来求解，最后用程序来验证我的结论，得到了一个较为满意的结果。我想这就是人们常说的举一反三的过程，拿到一个题目可以对其进行深入挖掘，做一道题会一类题，那绝对是一件极有意义，事半功倍的事。