采用线性SVM对线性不可分的数据进行分类（含matlab实现）

本文介绍一种常用的分类器设计技巧[1]：将线性不可分的数据映射到高维后，使其变得线性可分，然后利用前面介绍的线性分类器进行无（训练）误差分类。

假设我们有如下图所示的训练数据，如何对其进行分类？　显然，此时的正负样本是不可分的，因为无法找到一个超平面(由于此处是二维数据，超平面退化成直线）将其分开。

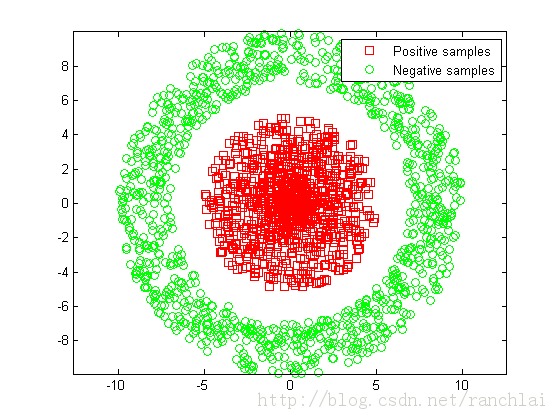
在这里介绍一个有用的技术：将二维数据转化成五维数据，即

　　　　（１）

举个列子，在一维的情况下，正样本1，-1和负样本0是线性不可分的，因为0在1和-1中间。映射成二维后，一定可以用一个直接将正负样本分开(为什么？）。这里其实隐含了一个ＶＣ维的概念在里面，暂时不讨论。

我们可以将正负样本都按照（１）式的方法映射成高维，然后对这些高维的数据进行线性ＳＶＭ分类，最终得到一个超平面。当新数据到来时，用同样的方法转成高维后代入超平面公式并判断其符号就能进行分类。所有的matlab代码如下：

%%
clc;
clear;
close all;


%% generate random data
n = 1000;
m = 1000;
x = GenCycleData(5,n)';
y = GenCyBandData(6,5,m)';




%%
%show the data
figure;
plot(x(1,:),x(2,:),'rs');
hold on;
plot(y(1,:),y(2,:),'go');
%title('2d training data');
legend('Positive samples','Negative samples');
axis equal




%%
%tranform to higher dimension


x1 = boost_data(x);
y1 = boost_data(y);


%%
%training..
for i=1:n
A(i,:) = [-x1(:,i)',-1];
end
for i=1:m
A(i+n,:) = [y1(:,i)',1];
end
c = ones(n+m,1)*(-1);


d = 5;


%% svm
H = eye(d+1);
H(d+1,d+1) = 0;
w = quadprog(H,zeros(d+1,1),A,c);
hold on;


%%
%show the trainig error
label_x = w'*[x1;ones(1,n)];
label_y = w'*[y1;ones(1,m)];


fprintf('true postive rate: %f\n',sum(label_x>0)/n);
fprintf('true negative rate: %f\n',sum(label_y<0)/m);

%% draw the hyper plan in 2D
fun = @(x,y) w(1)*x+w(2)*y+w(3)*x*y+w(4)*x^2+w(5)*y^2+w(6);
h = ezplot(fun,[-15,15,-15,15]);
set(h, 'Color', 'm');
title('classification result');

其中的boost_data将２Ｄ数据转成高维数据：

function [ x_out ] = boost_data(x)
N = size(x,2);
x_out = zeros(5,N);
x_out(1:2,:) = x;


for i=1:N
x_out(3,i) = x(1,i)*x(2,i);
x_out(4,i) = x(1,i)*x(1,i);
x_out(5,i) = x(2,i)*x(2,i);

end


end

最后的结果输出：

true postive rate: 1.000000
true negative rate: 1.000000

分类结果：

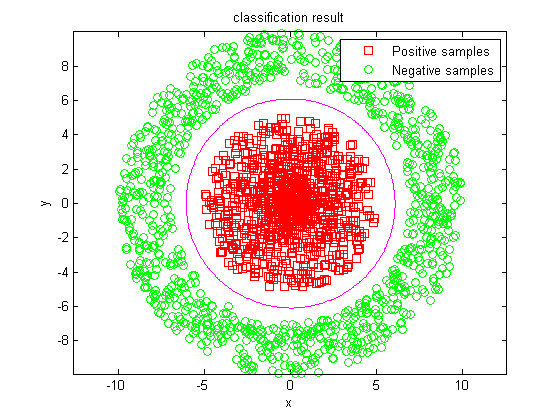
从上图可见，超平面在二维显示下是一个圆，并且该圆能最佳地将两组数据分开：圆处理正负样本的中心。

[1]Bishop, Christopher M., and Nasser M. Nasrabadi. Pattern recognition and machine learning. Vol. 1. New York: springer, 2006.