矩形的并的面积
描述在 X-Y 坐标平面上,给定多个矩形,它们的边分别与坐标轴平行。请计算它们的并的面积。
输入格式输入第一行为一个整数 n,1<=n<=100,表示矩形的数量。接下来有 n 行,每行包括四个数:x1,y1,x2,y2 (0<=x1<x2<=100000;0<=y1<y2<=100000),用空格分开,不一定为整数。(x1,y1)表示一个长方形的左下顶点坐标,(x2,y2)表示右上顶点坐标。
输出格式n个矩形的并的面积,保留两位小数。
输入样例20 0 2 2 1 1 3 3
输入第一行为一个整数 n,1<=n<=100,表示矩形的数量。接下来有 n 行,每行包括四个数:x1,y1,x2,y2 (0<=x1<x2<=100000;0<=y1<y2<=100000),用空格分开,不一定为整数。(x1,y1)表示一个长方形的左下顶点坐标,(x2,y2)表示右上顶点坐标。
输出格式n个矩形的并的面积,保留两位小数。
输入样例20 0 2 2 1 1 3 3
20 0 2 2 1 1 3 3
输出样例7.00
分析(离散化)
多个矩形重叠,重叠情况有很多种,不能进行直接计算,可以将二维坐标划分为一个个小的矩形,保证小矩形不存在重叠,然后对全部小矩形进行分析,将包含在原来题目给出的n个矩形中的小矩形标志,最后将标志的矩形面积相加就是结果;
怎么样进行二维坐标的划分呢?以所有的矩形边(4条)作为划分界线,可以保证到每个划分的小矩形都不重叠。如图:
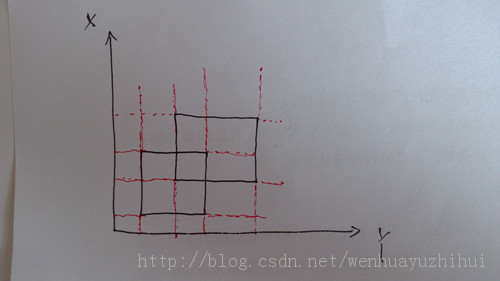
可以看出小矩形是不存在重复的。
下一步:将矩形的X坐标(每个矩形有两个)和Y坐标(两个)保存在X[] 数组 和Y[] 数组,并排序。
从图中可以看出,小矩形左下坐标位于大矩形类时 (X[i],Y[i])与 (X[i+1],Y[i+1])就是包含在大矩形类。
代码实现
#include<stdio.h>#include<stdlib.h> struct rectangle{ //结构体,保存矩形 float x1; float y1; float x2; float y2; }; rectangle arr[101]; float x[200];float y[200]; int flag[200][200];int Partition(float a[],int low,int high){ float pivotkey=a[low]; while(low<high){ while(low<high&&a[high]>=pivotkey) --high; a[low]=a[high]; while(low<high&&a[low]<=pivotkey) ++low; a[high]=a[low]; } a[low]=pivotkey; return low;}void QSort(float a[],int low,int high){ //快速排序 if(low<high){ int pivotloc=Partition(a,low,high); QSort(a,low,pivotloc-1); QSort(a,pivotloc+1,high); } } int main(){ float count=0; int n; int k=0; scanf("%d",&n); //数据输入 for(int i=0;i<n;i++){ scanf("%f",&arr[i].x1); scanf("%f",&arr[i].y1); scanf("%f",&arr[i].x2); scanf("%f",&arr[i].y2); x[k]=arr[i].x1; //保存所有X坐标到X[]数组,Y 到Y[]数组 y[k]=arr[i].y1; k++; x[k]=arr[i].x2; y[k]=arr[i].y2; k++; } QSort(x,0,2*n-1); //分别排序 QSort(y,0,2*n-1); for(int h=0;h<n;h++) //循环查找在矩形内的小矩形 for(int i=0;i<2*n;i++){ if(x[i]>=arr[h].x2) break; for(int j=0;j<2*n;j++){ if(y[j]>=arr[h].y2) break; if(x[i]>=arr[h].x1&&y[j]>=arr[h].y1) flag[i][j]=1; //符合,标志 } } for(int i=0;i<2*n;i++) //统计面积 for(int j=0;j<2*n;j++) count+=flag[i][j]*(x[i+1]-x[i])*(y[j+1]-y[j]); printf("%.2f",count); return 0; }
(离散化)

#include<stdio.h>#include<stdlib.h> struct rectangle{ //结构体,保存矩形 float x1; float y1; float x2; float y2; }; rectangle arr[101]; float x[200];float y[200]; int flag[200][200];int Partition(float a[],int low,int high){ float pivotkey=a[low]; while(low<high){ while(low<high&&a[high]>=pivotkey) --high; a[low]=a[high]; while(low<high&&a[low]<=pivotkey) ++low; a[high]=a[low]; } a[low]=pivotkey; return low;}void QSort(float a[],int low,int high){ //快速排序 if(low<high){ int pivotloc=Partition(a,low,high); QSort(a,low,pivotloc-1); QSort(a,pivotloc+1,high); } } int main(){ float count=0; int n; int k=0; scanf("%d",&n); //数据输入 for(int i=0;i<n;i++){ scanf("%f",&arr[i].x1); scanf("%f",&arr[i].y1); scanf("%f",&arr[i].x2); scanf("%f",&arr[i].y2); x[k]=arr[i].x1; //保存所有X坐标到X[]数组,Y 到Y[]数组 y[k]=arr[i].y1; k++; x[k]=arr[i].x2; y[k]=arr[i].y2; k++; } QSort(x,0,2*n-1); //分别排序 QSort(y,0,2*n-1); for(int h=0;h<n;h++) //循环查找在矩形内的小矩形 for(int i=0;i<2*n;i++){ if(x[i]>=arr[h].x2) break; for(int j=0;j<2*n;j++){ if(y[j]>=arr[h].y2) break; if(x[i]>=arr[h].x1&&y[j]>=arr[h].y1) flag[i][j]=1; //符合,标志 } } for(int i=0;i<2*n;i++) //统计面积 for(int j=0;j<2*n;j++) count+=flag[i][j]*(x[i+1]-x[i])*(y[j+1]-y[j]); printf("%.2f",count); return 0; }