算法之归并排序算法（merge sort）

归并排序算法

1.算法原理

---

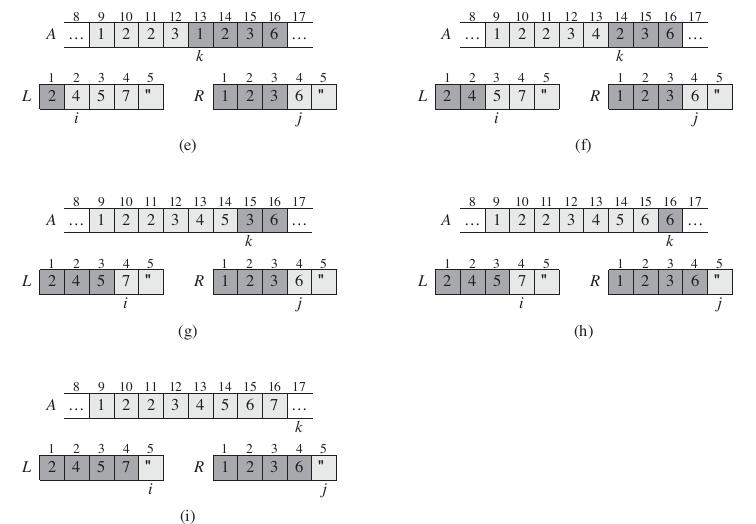
归并排序算法是分治法—ivide-and-Conquer）的典型应用。其操作的步骤如下：

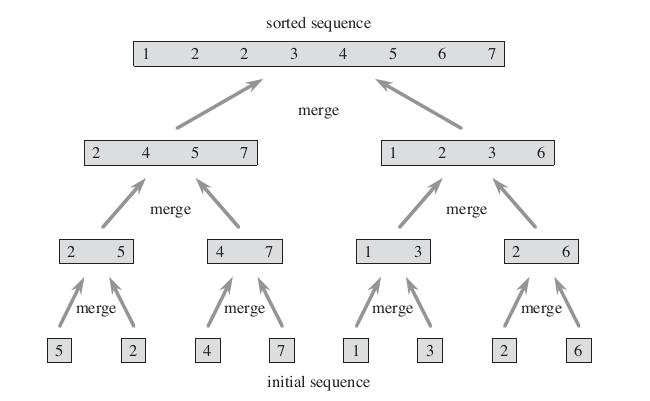
Divide：把n个元素的序列分为两个元素个数为n/2的子序列。Conquer：递归的调用归并排序算法对两个子序列进行排序Combine：对排好序的子序列进行合并，得到最后排序的结果。

归并算法用示意图表示如下：

归并排序算法的伪代码如下：

其中合并（MERGE）的伪代码如下：
#include <iostream>using namespace std;//将有二个有序数列a[first...mid]和a[mid...last]合并。void __merge(int a[], int first, int mid, int last, int temp[]){int i = first, j = mid + 1;int m = mid,   n = last;int k = 0;while (i <= m && j <= n){if (a[i] <= a[j])temp[k++] = a[i++];elsetemp[k++] = a[j++];}while (i <= m)temp[k++] = a[i++];while (j <= n)temp[k++] = a[j++];for (i = 0; i < k; i++)a[first + i] = temp[i];}void __merge_sort(int a[], int first, int last, int temp[]){    if(first < last)    {        int mid = (first + last) / 2;        __merge_sort(a, first, mid, temp);        __merge_sort(a, mid + 1, last, temp);        __merge(a, first, mid, last, temp);    }}bool MergeSort(int a[], int n){    int *p = new int[n];    if(p == NULL)    {        return false;    }    else    {        __merge_sort(a, 0, n - 1, p);        delete[] p;        return true;    }}int main(){    const int LEN = 10;    int a[LEN] = {23, 40, 45, 19, 12, 16, 90, 39, 87, 71};    cout << "Before the merge sort, the Array is:" << endl;    for(int i = 0; i < LEN; ++i)    {        cout << "a[ " << i + 1 << " ] is: "<< a[i] << endl;    }    cout << endl;    MergeSort(a, LEN);    cout << "After the merge sort, the Array is:" << endl;    for(int i = 0; i < LEN; ++i)    {        cout << "a[ " << i + 1 << " ] is: "<< a[i] << endl;    }    return 0;}

3.算法复杂度
该算法的时间复杂度为O(nlogn)
4.内容来源
教材：Introduction to Algorithm 3rd Edition 
白话经典算法系列之五 归并排序的实现
链接：白话经典算法系列之五 归并排序的实现