我要学会“割舍”

今年我新接的班是五（7）班，我担任本班数学课。屈指算来，到目前为止，跟孩子们朝夕相处将近4个月，在这四个月中，我尽力了解、掌握每个孩子的学习情况（包括过去学习情况、已有学习习惯、新知接受能力、家庭情况等）。经过4个月的朝夕相处，虽然对每个学生整体情况都有所了解，但毕竟时间较短，所以对孩子的学习状况总有些不放心，有时会出现关爱过度，包办代替。例如： 以前在布置作业时，对于作业中出现有难度的题目，我会提前给学生提示、启发，甚至讲解，因为我对学生存在顾虑，担心学生不会做，家长指导不到位或指导方式欠佳。我也知道这种做法不妥，会扼杀学生独立思考的良机，会滋生懒学生的惰性，但我的这份“过度关爱”的理念往往占据上风，支配我的行动。造成强势老师，这样的强势老师务必会培养出弱势的学生，但两天前留的一次家庭作业彻底扭转了我的想法，它使我痛下决心---要学会“割舍”。

两天前，我留的家庭作业是智力开发报，智力开发报最后一道压轴题是： 一个长方形的底面积是40平方分米，底面周长是26分米，高是4分米。求这个长方体的表面积和体积。我阅读此题后，我想，这道题求体积时，学生应该都会，至于求表面积，有些难度，估计有些孩子不会做，这给学生提示与否？在经过思维的挣扎后，决定放手一次，看看到底有多少孩子动脑思考？第二天在处理到此题时，我决定让学生回答解题思路---说出算式及每一步求的是什么。下面是张世辰与我的对话：

辰：（8×5+5×4+8×4)×2=184（平方分米）。

师； 8和5从哪里来，8和5各代表什么？

辰：计算得到的，8是长，5是宽。

师：你是怎样计算的？

辰：8+5=13,8×5=40

师：13从哪里来？做题要有依据。

辰；周长26÷2=13,13是长与宽的和。

师：你的回答很精彩，不过写过程时，最好写清楚些，我们数学讲究要有根有据。你看这样是否更清楚些，说着我们师生共同完成此题解题过程。张世辰满意的笑了。

这时张赛博举手，要讲述他的解题思路：

博：13×4×2=104（平方分米）

师：13×4求的是什么？

孩子的回答含糊不清（看来心中知道，就是用语言回答不完整；也可能是家长辅导的）。

师：启发，你求的是不是长方体的侧面积？

博：高兴地说：“是，是”

为了让学生对这种解题思路更清晰，我随机找了一个长方体的盒子，把它展开，去掉上面，让学生只观察四个侧面。我提示：把四个侧面按“长×高+宽×高分”成面积相等的2组。看其中的一组的面积，边说边把宽×高的面撕下来，和长×高拼在一起，这样就组成了一个新的长方形，新长方形的长是13分米，宽是4分米。把图贴在黑板上。

这时，听到孩子不由自主地发出“哦，原来是这样呀。”的声音，看来此时是真正明白了13×4的具体意义了，再求长方体的表面积就迎刃而解了。

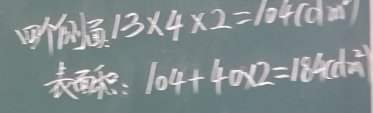
我对张赛博同学进行了表扬，谁知，这时又有一位同学在下面喊：老师，老师，还有一种解题方法。我循着声音望去，只见李子恒把手就得很高，屁股已经离开了凳子，马上要站起来，其他学生也向他投去不解的目光。我示意让李子恒回答，李子恒很快说出算式：

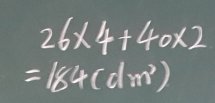
并解释：26×4求的是四个侧面的面积，40×2求的是上下底面的面积。我首先肯定李子恒的想法是正确的，但这种解法不好理解，我就“26×4”求的是四个侧面积进行了启发引导。

师：大家想：四个侧面我们能不能把它们看成是四个小长方形？

生：学生们点头同意，可以

师：每个小长方形的面积怎样求？

生：长×宽

师：它们的宽有什么特点？

生：都是4分米

师：关键是求它们的长。

生：对。

师：怎样求这四个长方形的长呢？

这时我听到有一位学生说：“它们长的和是26厘米”。

师：我们可以把这四条长分别用a1、a2、a3、a4来表示，由题意可知a1+a2+a3+a4=26厘米，每个小长方形的面积是多少呢？

生：分别是a1×4、a2×4、a3×4、a4×4

师：它们的面积和如何表示？

生：把“a1×、a2×4、a3×4、a4×4 ”加起来

即a1×4 + a2×4 + a3×4 + a4×4

师：a1×4 + a2×4 + a3×4 + a4×4采用乘法分配律可得：（ a1+a2+a3+a4）×4，又知道a1+a2+a3+a4=26，所以这四个小长方形的面积和就是：26×4。此时，学生才恍然大悟，真正明白了26×4的真正意义。

从中可以看出，学生的思维火花需要的是启发、点燃，该放手的时候一定要放手。他像一位刚刚学走路的孩子，如果大人不放心，恐怕孩子磕着，碰着，不舍得放手，孩子永远也学不会走路，只有我们学会割舍，“狠下心来”不怕孩子跌倒，他们才能快速学会走路。学习亦是如此，学生不能做温室的花朵，要做阳光下的小花，学生不是捧在手中的花瓶，而是生活中的水杯，我们要把握好适度，要学会“割舍”。