我给阿基米德当助手

不用说，我就知道，你一定很吃惊，我怎么可能给两千多年前古希腊的大数学家阿基米德当助手呢？

当然咯，我绝对回不到他那个年代，也绝对听不到他那句“给我一个支点，我就能够撬起整个地球”的豪言壮语。但是，我确确实实当了一回他的助手。

怎么当的？听我慢慢道来。

过年这几天，我除了到外婆家尝尝丰盛的饭菜，随爸妈到紫荆山公园散散步，就是赶语文老师布置的寒假作业——精读《西游记》，每读一回做一篇小摘记。写累了，就翻翻“可怕的科学
经典数学”系列书。无意间翻到一章，讲的全是“球体积”的知识。要说，我学过球面积的运算方法后，一直想了解球体积该如何计算。真巧，想啥来啥，我便仔细阅读起来。

哦，我终于明白了。原来数学家们早就列出了球体积的计算公式：ν=4／3πr³，即三分之四乘圆周率乘半径的三次方。我随意找了几个数字当r，代入公式玩了玩。嗯，挺有意思，乒乓球能算，玻璃球也能算。

当然，最让我感兴趣的，还是书中的有一段。讲的什么呢？是讲阿基米德对球体积计算的思考。经过无数次的实验，他得出一个结论：球体积等于刚好能放进该球体的圆柱体体积的2/3。这个结论使我非常好奇，好奇得心里直痒痒。

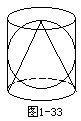书上还有一幅说明这个结论的图像，并说这个图像被画在阿基米德的墓碑上。然而，书上没有举例证明这个结论的正确性。真的成立吗？哦，我决定当一回阿基米德的助手，来帮他验证一下。

我找来一个实心球，又拿张大纸，卷成一个直径和高与实心球直径一般长的圆柱体，再把实心球放进去。随后，开始计算。

我把实心球的半径r设为3（圆柱体的半径同样为3，高则为6）。先算圆柱体的体积（计算公式为底面积×高），底面积为圆周率乘半径的平方：3.14×3²=28.26。再乘6，得169.56。那么，实心球的体积就是169.56×2/3=113.04。

再用数学家们提供的公式算一遍：ν（实心球体积）=4／3πr³=4／3×3.14×3³=113.04。咦，神了，真是一样哦！

伟大的阿基米德呀，我真是佩服您了，崇敬您了！给您当一回助手，真是荣幸哟！